设{an},{bn},{cn}均为非负数列,且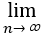 an=0,
an=0, 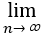 bn=1,
bn=1,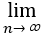 cn=∞,则必有【 】
cn=∞,则必有【 】
A、an<bn对任意n成立
B、bn<cn对任意n成立
C、极限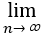 ancn不存在
ancn不存在
D、极限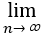 bncn不存在
bncn不存在
设{an},{bn},{cn}均为非负数列,且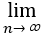 an=0,
an=0, 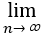 bn=1,
bn=1,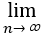 cn=∞,则必有【 】
cn=∞,则必有【 】
A、an<bn对任意n成立
B、bn<cn对任意n成立
C、极限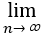 ancn不存在
ancn不存在
D、极限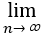 bncn不存在
bncn不存在
D
【解析】
利用极限的性质可以证明: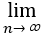 bncn=∞.
bncn=∞.
若取an=cn=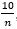 ,bn=1,可以证明另三个选项不正确.
,bn=1,可以证明另三个选项不正确.
当x→0时,用“o(x)”表示比x高阶的无穷小,则下列式子中错误的是【 】
设{an},{bn},{cn}均为非负数列,且an=0, bn=1,cn=∞,则必有【 】
设{an},{bn},{cn}均为非负数列,且an=0, bn=1,cn=∞,则必有【 】
设{an},{bn},{cn}均为非负数列,且an=0, bn=1,cn=∞,则必有【 】
设{an},{bn},{cn}均为非负数列,且an=0, bn=1,cn=∞,则必有【 】
设{an},{bn},{cn}均为非负数列,且an=0, bn=1,cn=∞,则必有【 】
设{an},{bn},{cn}均为非负数列,且an=0, bn=1,cn=∞,则必有【 】