设f(x)在x=0处连续，且对任意的x∈R，有f(x)=f(3x)，证明：f(x)是常值函数.
-
关注优题吧，注册平台账号.
题吧，智能辅助学习中心
证明题（2022年天津大学）
答案解析
由于f(x)在x=0处连续，故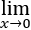
f(x)=f(0)，对∀x∈R
f(x)=f(x/3)=f(x/32)=⋯=f(x/3n)=⋯
∴f(x)=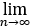
f(x/3n)=f(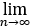x/3n)=f(0)
故f(x)≡f(0).
讨论
已知函数f(x)为(A,B)上的连续函数，且有[a,b]⊂(a,b)，证明：1/h [f(x+h)-f(x)]dx=f(b)-f(a)
解答如下问题：(1)证明：(-1)n n(n+1)/(n(n+1) x2+2n)关于x∈(-∞,+∞)一致收敛.(2)计算(-1)n n(n+1)/(n(n+1) x2+2n ).
求(x2+y2+z2 )2=4(x2+y2-z2)所围立体的体积.
证明：f(x)=tx-1 e-t lntdt 在(0,+∞)上连续.
已知S:(x-5)2+2y2+2(z+1)2=3，方向取外侧，计算∬S((x-5)dydz+ydzdx+zdxdy)/[(x-5)2+y2+z2 ](3/2)
若函数f(x)在[0,1]上连续，f(0)=0,f(1)=1，则对任何自然数n≥1，存在ξ_n∈[0,1]，使得f(ξn+1/n)=f(ξn )+1/n.
已知函数f(x)在[a,+∞)上连续，且f(x)存在，证明：(1)函数f(x)有界；(2)存在ξ∈[a,+∞)，使得f(ξ)为f(x)在[a,+∞)上的最大值或最小值.
验证函数f(x)=lnx在区间[1,+∞)上一致连续，但在(0,1)上不一致连续.
设函数f(x)在(0,1)上有定义，且函数exf(x)与函数e-f(x)在(0,1)上都是单调递增的，求证：f(x)在(0,1)上连续.
设f(x)在(a,b)上一致连续，则f(x)在(a,b)上有界.