已知函数f(x)在[a,b]上可积,且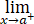 f(x)=A.对任意的h∈(0,1),设非负函数g(x,h)满足:
f(x)=A.对任意的h∈(0,1),设非负函数g(x,h)满足: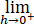
 g(x,h) dx=1,若对任意的c∈(a,b),g(x,h)在当h→0+关于 x∈[c,b]一致收敛于0,即对∀ε>0,∃δ>0,当0<h<δ时,对∀x∈[c,b]有|g(x,h)|<ε,证明:
g(x,h) dx=1,若对任意的c∈(a,b),g(x,h)在当h→0+关于 x∈[c,b]一致收敛于0,即对∀ε>0,∃δ>0,当0<h<δ时,对∀x∈[c,b]有|g(x,h)|<ε,证明:
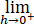
 f(x)g(x,h)dx=A
f(x)g(x,h)dx=A
已知函数f(x)在[a,b]上可积,且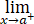 f(x)=A.对任意的h∈(0,1),设非负函数g(x,h)满足:
f(x)=A.对任意的h∈(0,1),设非负函数g(x,h)满足: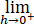
 g(x,h) dx=1,若对任意的c∈(a,b),g(x,h)在当h→0+关于 x∈[c,b]一致收敛于0,即对∀ε>0,∃δ>0,当0<h<δ时,对∀x∈[c,b]有|g(x,h)|<ε,证明:
g(x,h) dx=1,若对任意的c∈(a,b),g(x,h)在当h→0+关于 x∈[c,b]一致收敛于0,即对∀ε>0,∃δ>0,当0<h<δ时,对∀x∈[c,b]有|g(x,h)|<ε,证明:
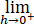
 f(x)g(x,h)dx=A
f(x)g(x,h)dx=A
由已知:A=A∙g(x,h) dx,故只需证明:(f(x)-A)g(x,h) dx=0即可.|(f(x)-A)g(x,h) dx|≤|(f(x)-A)g(x,h) dx|+|(f(x)-A)g(x,h) dx|≤|f(x)-A|g(x,h) dx+|f(x)-A|g(x,h) dx令c-a<h,则当h→0+时,c→a+,∵f(x)=A∴对∀ε>0,∃δ1>0,当0<x-a<h<δ1时,|f(x)-A|<ε.又g(x,h) dx<g(x,h) dx,且g(x,h) dx=1,由极限保号性知,对上述ε,∃δ2,当0<h<δ2时,有g(x,h) dx<3/2取δ_3=min{δ1,δ2...
查看完整答案