大学数学-考研试题(理工数学Ⅰ 2021年函数极限存在准则)

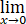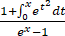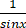计算题（2021年理工数学Ⅰ；2021年理工数学Ⅱ）

求极限( - ).

答案解析

( - ) =

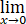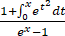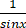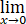
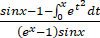
又因为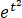dt = (1+t²+o(t²))dt = x+1/3·x³+o(x³)，故

原式 =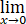

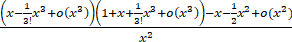
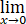
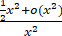= = 1/2.

讨论

函数极限

求(2sinx+cosx)1/x

设[(x+2a)/(x-a)]x=8，则a=________.

已知((x+a)/(x-a))x =9，求常数a.

(+-2)/x2=__________.

(1/x2 -1/xtanx)=______.

设f(x)/lnx=1，则【】

((1+ex)/2)cotx=__________.

求极限sin4x/(-1)

(xk-1)/(xλx-1)，其中k是正整数，λ≠0是常数.

计算(2-x-2cosx)/(xex-ln⁡(1+x))

函数与极限

由下面哪个条件能够判断{xn}收敛【】

对有界数列{xn}，下面哪个说法可作为xn=L的定义【】（此题不全，待更新）

设f(x)=sin⁡(a1 x)+sin⁡(a2 x)+sin⁡(a3 x),a1,a2,a3>0.证明：存在数列{tn}使得tn=+∞且f(x+tn)=f(x)对∀x∈R一致成立.

求证：((cosx)ndx)1/n =1

求证：(n/3-k2/n2 )=-1/2.

设an=a,且a≠0，则当n充分大时，有【】.

设{an}，{bn}，{cn}均为非负数列，且an=0， bn=1，cn=∞，则必有【】

考研数列极限存在准则

设函数f(x)在（-∞,+∞）内单调有界，{xn}为数列，下列命题正确的是【】

设数列{xn}满足0<x1<π，xn+1=sinxn（n=1,2,...）.证明xn存在，并求该极限.

函数极限存在准则

已知 fn(x)=求证：（1）对于任何自然数n，方程fn(x)=在区间(0,)中仅有一根；（2）设xn∈(0,)满足fn(xn)=，则.

设函数f:R→R满足：(1) f(1)=1,(2) f'(x)=1/(x2+[f(x)]2),∀x≥1.证明：f(x)存在且小于1+π/4.

设函数f(x)=x-[x]，其中[x]表示不超过x的最大整数，求极限1/xf(x)dx.

已知函数f(x)在[a,b]上可积，且f(x)=A.对任意的h∈(0,1)，设非负函数g(x,h)满足：⁡g(x,h) dx=1，若对任意的c∈(a,b),g(x,h)在当h→0+关于 x∈[c,b]一致收敛于0，即对∀ε>0,∃δ>0，当0<h<δ时，对∀x∈[c,b]有|g(x,h)|<ε，证明：f(x)g(x,h)dx=A

确定常数a,b，使得极限(axcosx-bsinx)/x³ 存在，并求极限.

当x→1时，函数(x2-1)/(x-1) e1/(x-1)的极限【】

x∙cos(1/x)= 【】

已知⁡[aarctan + ]存在，求a的值.

设X1,X2,…,Xn为来自均值为θ的指数分布总体的简单随机样本，Y1,Y2,…,Ym为来自均值为2θ的指数分布总体的简单随机样本，且两样本相互独立，其中θ(θ>0)是未知参数.利用样本X1,X2,…,Xn,Y1,Y2,…,Ym求θ的最大似然估计量θ ̂，并求D(θ ̂).

二次型f(x1,x2,x3 ) = (x1 + x2)2 + (x2 + x3)2 - (x3 - x1)2的正惯性指数依次为【】