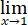大学数学-考研试题(同济大学 2022年两个重要极限)

计算题（2022年同济大学）

(x^k-1)/(x^λx-1)，其中k是正整数，λ≠0是常数.

答案解析

使用洛必达法则，分别对分子、分母求导，

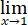(x^k-1)/(x^λx-1)=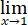(kx^k-1)/(x^λx [λlnx+λ])=k/λ.

讨论

函数极限

东北财经大学两个重要极限

sin(x2-1)/(x-1)=__________。

求极限⁡( - ).

求(1/x-1/(ex-1)).

求(cos√x)π/x

当x→1时，函数(x2-1)/(x-1) e1/(x-1)的极限【】

求(2sinx+cosx)1/x

设[(x+2a)/(x-a)]x=8，则a=________.

已知((x+a)/(x-a))x =9，求常数a.

(+-2)/x2=__________.

两个重要极限

(1/x2 -1/xtanx)=______.

求极限sin4x/(-1)

考研两个重要极限

求f(x)=的表达式，并作函数f(x)图像。

证明：[x3]+x2=[x2]+x3存在一个非整数解，其中[x]表示不大于x的最大整数.

求⁡(ex-sinx-1)/(1-).

(1/√x)tanx =__________.

求(sin⁡(2/x)+cos(1/x))x

cotx(1/sinx-1/x)=________.

(1+3x)2/sinx=__________.

函数与极限

((n-2)/(n+1))n=________.

设f(x)有连续的导数，f(0)=0,f'(0)≠0,F(x)=(x2-t2) f(t)dt，且当x→0时，F'(x)与xk是同阶无穷小，则k等于【】

求⁡[sin⁡(π/n)/(n+1)+sin(2π/n)/(n+1/2)+⋯+sinπ/(n+1/n)]

设 f(x) 是连续函数，F(x)是 f(x)的原函数，则【】

设-π/2≤xn≤π/2，则【】

当x→0时，α(x),β(x)是非零无穷小量，给出以下四个命题①若α(x)~β(x)，则α2 (x)~β2 (x)②若α2 (x)~β2 (x)，则α(x)~β(x)③若α(x)~β(x)，则α(x)-β(x)=o(α(x))④若α(x)-β(x)=o(α(x))，则α(x)~β(x)其中所有真命题的序号是【】

已知an=-(-1)n/n(n=1,2,…)，则{an}【】

对有界数列{xn}，下面哪个说法可作为xn=L的定义【】（此题不全，待更新）

设函数f(x)在[a,b]上有定义，在(a,b)上连续.下面哪个条件能够判定函数f(x)在[a,b]上有最大值【】

设函数f:R→R满足：(1) f(1)=1,(2) f'(x)=1/(x2+[f(x)]2),∀x≥1.证明：f(x)存在且小于1+π/4.