设函数f(x)在区间(-∞,+∞)绝对可积,函数g(x)在区间(-∞,+∞)有界且满足:|g(x)-g' (x)|≤L|x-x' |,L>0是常数.
证明:函数F(y)=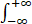 f(x)g(x)dx在区间(-∞,+∞)上一致连续.
f(x)g(x)dx在区间(-∞,+∞)上一致连续.
设函数f(x)在区间(-∞,+∞)绝对可积,函数g(x)在区间(-∞,+∞)有界且满足:|g(x)-g' (x)|≤L|x-x' |,L>0是常数.
证明:函数F(y)=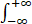 f(x)g(x)dx在区间(-∞,+∞)上一致连续.
f(x)g(x)dx在区间(-∞,+∞)上一致连续.
暂无答案
证明:f(x)=tx-1 e-t lntdt 在(0,+∞)上连续.
设函数f(x)在(0,1)上有定义,且函数exf(x)与函数e-f(x)在(0,1)上都是单调递增的,求证:f(x)在(0,1)上连续.
设f(x)在(a,b)上一致连续,则f(x)在(a,b)上有界.
设函数f(x)在[0,+∞)连续,(f(x)-k√x)=0,k>0为常数,证明:f(x)在[0,+∞)上一致连续.
试问函数f(x,y)=sin[π/(1-x2-y2 )]在区域D:{(x,y)∈R2;x2+y2<1}上是否一致连续?证明你的结论.
设f(x)在x=0处连续,且对任意的x∈R,有f(x)=f(3x),证明:f(x)是常值函数.
给定x0>0以及[0,+∞)上连续函数f(x),证明:至多具有一个定义于[0,+∞)上的连续函数y(x)满足对任意的x>0,有dy/dx=-y³+f(x),其中y(0)=y0.
已知函数f(x)在[a,+∞)上连续,且f(x)存在,证明:(1)函数f(x)有界;(2)存在ξ∈[a,+∞),使得f(ξ)为f(x)在[a,+∞)上的最大值或最小值.