大学数学-竞赛试题(南京工业大学 2009年数列极限存在准则)

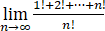
计算题（2009年南京工业大学）

求

答案解析

原式=1+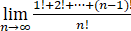，由于

0<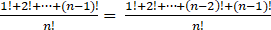

<<=

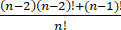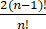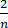
因为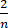→0，由夹逼准则得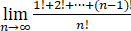=0

故原式=1+0=1.

讨论

数列极限存在准则

求证：((cosx)ndx)1/n =1

求证：(n/3-k2/n2 )=-1/2.

设x1=10,xn+1=(n=1,2,⋯)，试证数列{xn}的极限存在，并求此极限.

设-π/2≤xn≤π/2，则【】

已知an=-(-1)n/n(n=1,2,…)，则{an}【】

对有界数列{xn}，下面哪个说法可作为xn=L的定义【】（此题不全，待更新）

设f(x)=sin⁡(a1 x)+sin⁡(a2 x)+sin⁡(a3 x),a1,a2,a3>0.证明：存在数列{tn}使得tn=+∞且f(x+tn)=f(x)对∀x∈R一致成立.

已知an=+∞，证明(a1+a2+⋯+an)/n=+∞，并举例说明反过来不成立.

证明数列{sinn}发散.

设数列{xn}满足1/xn+1 +lnxn<1，证明：xn存在，并求之.(已知：1/x+lnx≥1)

数列极限

设0<a<1，求极限(a+2a2+3a3+⋯+nan).

求⁡[sin⁡(π/n)/(n+1)+sin(2π/n)/(n+1/2)+⋯+sinπ/(n+1/n)]

已知an=a≠0，试用ε-N语言证明：1/an =1/a.

设an=a,且a≠0，则当n充分大时，有【】.

设{an}，{bn}，{cn}均为非负数列，且an=0， bn=1，cn=∞，则必有【】

设函数f(x)在（-∞,+∞）内单调有界，{xn}为数列，下列命题正确的是【】

设数列{xn}满足0<x1<π，xn+1=sinxn（n=1,2,...）.证明xn存在，并求该极限.

莫斯科公路学院数列极限存在准则

莫斯科电子技术学院数列极限存在准则

莫斯科民族友谊大学数列极限存在准则

函数与极限

已知φ(x)=|x-t|f(t)dt，若积分存在，且f(x)>0，证明：φ(x)为[a,b]上的凸函数.

当x→0时，函数f(x)=ax+bx2+ln⁡(1+x)与g(x)=ex^2 -cosx是等价无穷小，则ab=______.

已知{xn },{yn}满足x1=yn=1/2,xn+1=sinxn,yn+1=yn2 (n=1,2,⋯) ，则当n→∞时【】

当x→0时，用“o(x)”表示比x高阶的无穷小，则下列式子中错误的是【】

考研无穷小与无穷大

设a≠，则ln= .

已知函数f(x)是周期为π的奇函数，且当x∈（0，π/2）时f(x)=sinx-cosx+2，则当x∈（π，π/2）时f(x)=____________________.

函数y=sinx|sinx|（其中|x|≤π/2）的反函数为____________________.

设函数f(x)在[a,b]上有定义，在(a,b)上连续.下面哪个条件能够判定函数f(x)在[a,b]上有最大值【】

若函数f(x)在[0,1]上连续，f(0)=0,f(1)=1，则对任何自然数n≥1，存在ξ_n∈[0,1]，使得f(ξn+1/n)=f(ξn )+1/n.