考研2025年理工数学Ⅰ( )
设x1,x2,⋯,xn为来自总体N(μ,2)的简单随机样本,记X ̅=1/n  xi ,Zα表示标准正态分布的上侧α分位数,假设检验问题:H0:μ≤1,H1:μ>1的显著性水平为α的检验的拒绝域为【 】
xi ,Zα表示标准正态分布的上侧α分位数,假设检验问题:H0:μ≤1,H1:μ>1的显著性水平为α的检验的拒绝域为【 】
A、{(x1,x2,⋯xn )│X ̅>1+2/n Zα }
B、{(x1,x2,⋯xn )│X ̅>1+√2/n Zα }
C、{(x1,x2,⋯xn )│X ̅>1+2/√n Zα }
D、{(x1,x2,⋯xn )│X ̅>1+√(2/n) Zα }
解答过程见word版
考研1998年理工数学Ⅰ( )
设某次考试的学生成绩服从正态分布,从中随机地抽取36位考生的成绩,算得平均成绩为66.5分,标准差为15分.问在显著性水平0.05下,是否可以认为这次考试全体考生的平均成绩为70分?并给出检验过程.
附表:t分布表 P{t(n)≤t_p (n)}=p
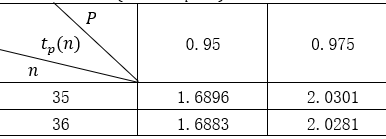
设该次考试全体考生的成绩为总体X,则X~N(μ,σ2 ),σ2未知.把从X中抽取的容量为n的样本均值记为X ̅,样本标准差记为s,在显著性水平α=0.05下检验假设:
H0:μ=70;H1:μ≠70,
选取检验统计量 T=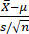 ~t(n-1),
~t(n-1),
则拒绝域为:|t|=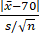 ≥t_(1-α/2) (n-1),
≥t_(1-α/2) (n-1),
由已知有:x ̅=66.5,n=36,s=15,α=0.05,t1-α/2(n-1)=t0.975 (35)=2.0301,算得
|t|=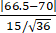 =1.4<2.0301.
=1.4<2.0301.
所以接受假设H0:μ=70,即在显著性水平α=0.05下,可以认为这次考试全体考生的平均成绩为70分.
竞赛2020年3月阿里巴巴( )
蚂蚁森林是全球最大的个人碳账户平台,该平台以量化方式记录每个人的低碳行为。当支付宝用户收集到足够的“能量”时,他/她可以向蚂蚁森林申请种植一棵真正的树。截至2019年4月22日(世界地球曰),支付宝蚂蚁森林的5亿用户已经在中国西北地区种植了1亿棵真树,总面积为11.2万公顷,保护着总面积为1.2万公顷的保护地。
1.本题两小问中考虑在一个3×4的长方形区域的每个小方格的中心点种树,要求在横、竖、斜3个方向上都不能存在连续的3颗(及以上)树。令1表示可以种树,0表示不可以种树。满足种树条件的示意图为
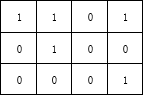
不满足种树条件的示意图为
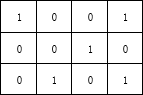
(a)请问在一个3×4的区域里,最多能种多少颗树,并给出一种种植的方式。
(b) 在满足上一问最多能种多少颗树答案的前提下,请问一共有多少种种法,给出思路和答案。
2. 考虑一个由从左到右的n个小方格组成的1×n的区域,从左向右依次在每个小方格种一棵树,一共种n棵。树的种类只有两种:胡杨和樟子松。假设在第一个小方格种植的树是胡杨的概率是r。后续种树的规则为:如果前一个小方格种的是胡杨,则本格种胡杨的概率为s;如果前一个小方格种的是樟子松,则本格种樟子松的概率为t,0<r,s,t<1。
(a)假设r=1/3,s+t≠1。是否存在s和t,使得对任意的i,2≤i≤n,在第i个小方格种植的树是胡杨的概率都等于一个跟i无关的常数?如果存在,请给出s和t的关系;如果不存在,请说明理由。
(b) 假设r=1/3,s=3/4,t=4/5。假设我们观察到第2019个小方格里种植的树是胡杨,但我们观察不到在其它小方格里种植的是哪种树。请问在第一个小方格里种植的树是胡杨的概率是多少?
3.为了种树的可持续发展控制成本,蚂蚁森林希望在知道用户申请数量之前从公益机构获得种植配额。令随机变量D1和D2分别表示支付宝用户对胡杨和樟子松的申请数量。将Di的分布函数记为Fi,其均值和方差分别表示为μi和σi2(i=1,2)。
假设蚂蚁森林只知道μi和σi2 (i=1,2)但并不知道F的其它信息。蚂蚁森林需要确定两种树的配额,分别记为Qi (i=1,2)。由于环境的承受能力,种植的树木总数不能超过给定的常数M,即
Q1+Q2≤M
并且假设M≥μ1+μ2。
已知两种树的订购成本分别为cQi (i=1,2)。如果预留配额Qi小于种树申请数量Di,即Qi≤Di,则增加额外成本m[Di-Qi ]+ (i=1,2)。这里[x]+≜max{x,0}.m,c,μi,σi为已知常数且满足关系(m-c)/c>(σ1/μ1 )2>(σ2/μ2 )2.
蚂蚁森林希望选择种树配额Qi≥0(i=1,2)使得在最坏情况下总成本的期望极小,其中最坏情况是针对所有可能的均值为μi、方差为σi2的分布函数Fi。从数学上讲,目标是求解以下优化问题:
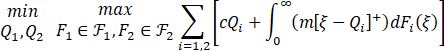 ,(1)
,(1)
subject to Q1+Q2≤M,Q1,Q2≥0
其中Fi是所有均值为μi、方差为σi2 (i=1,2)的累积分布函数的集合,其支撑集为非负数。
问题:请求解问题(1),推导最优种树配额Qi,i=1,2的显式表达式。
考研2021年理工数学Ⅰ( )
设X1,X2,…,X16为来自总体N(μ,4)的简单随机样本.考虑假设检验问题:H0:μ≤10,H1:μ>10.Φ(x)表示标准正态分布函数,若该检验问题的拒绝域为W={X ̅≥11},其中X ̅=1/16·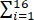 Xi ,则μ=11.5时,该检验犯第二类错误的概率为【 】
Xi ,则μ=11.5时,该检验犯第二类错误的概率为【 】
A、1 - Φ(0.5)
B、1 - Φ(1)
C、1 - Φ(1.5)
D、1 - Φ(2)

