设f(t)=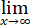
t(1+1/x)2tx ，则f' (t)=__________.
-
关注优题吧，注册平台账号.
题吧，智能辅助学习中心
设函数g(x)在x=0的领域内有定义，g(0)=g'(0)=0,f(x)=，求f'(0).
设y=etan(1/x) ∙sin(1/x)，则y'=________________.
设f(t)=t(1+1/x)2x，则f' (t)=________________.
设f(x)=x(x+1)(x+2)∙⋯∙(x+n)，则f'(0)=____________.
设y=ln(1+ax)，其中a是非零常数，则y'=__________，y''=__________.
设α1=,α2=,α3=，则三条直线a1 x+b1 y+c1=0,a2 x+b2 y+c2=0,a3 x+b3 y+c3=0,(其中ai2+bi2≠0,i=1,2,3)相交于一点的充要条件是【 】
设当x=0时，f(sinx)= f2(sinx)，f'(x)≠0，则f(0)=__________.
已知函数y=f(x)在x=2处连续，且=2求证f(x)在x=2处可导，并求f'(x)=2.
证明：两条心脏线ρ=α(1+cosθ)与ρ=α(1+cosθ)在交点处的切线相互垂直.
设y=y(x)由方程xef(y)=eyln29确定，其中具有二阶导数，f'≠1，则= ____________________.
若f(x)在x0的领域内有定义，在x0可导，则f(x)在x0的某领域内连续.
若f(x),g(x)在[a,b]上可导，∀x∈[a,b],f' (x)≤g'(x)，则∀x∈[a,b],f(x)≤g(x).
设f(x)在[a,b]上单调，证明其变上限积分F(x)=f(t)dt在每一x∈(a,b)的单侧导数F+'(x),F_'(x)均存在.
设B是秩为2的5×4矩阵，α1=(1,1,2,3)T,α2=(-1,1,4,-1)T,α3=(5,-1,-8,9)T是齐次线性方程组Bx=0的解向量，求Bx=0的解空间的一个标准正交基.
函数f(x)=(x2-x-2)|x3-x|不可导点的个数是【 】
已知函数y=y(x)在任意点x处的增量Δy=yΔx/(1+x2)+α，且当Δx→0时，α是∆x(∆x→0)的高阶无穷小，y(0)=π，则y(1)等于【 】
确定常数λ，使在右半平面x>0上的向量A(x,y)=2xy(x4+y2 )λ i-x2 (x4+y2 )λ j为某二元函数u(x,y)的梯度，并求u(x,y).
计算曲面积分I=∬Σ (axdydz+(z+a)2dxdy)/(x2+y2+z2 )1/2 ，其中Σ为下半球面z=-的上侧，a为大于零的常数.
设y=y(x),z=z(x)是由方程z=xf(x+y)和F(x,y,z)=0所确定的函数，其中f和F分别具有一阶连续导数和一阶连续偏导数，求dz/dx.