设变换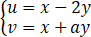
可把方程6 ∂2z/∂x2 +∂2z/∂x∂y-∂2z/∂x∂y=0化简为∂2z/∂u∂v=0，求常数a，其中z=z(x,y)有二阶连续的偏导数.
-
关注优题吧，注册平台账号.
题吧，智能辅助学习中心
问答题（1996年理工数学Ⅰ）
答案解析
∂z/∂x=∂z/∂u+∂z/∂v,∂z/∂y=-2 ∂z/∂u+a ∂z/∂v,∂2 z/∂x2=∂2z/∂u2+2∂2z/∂u∂v+∂2z/∂v2,∂2 z/∂x∂y=-2 ∂2z/∂u2+(a-2) ∂2z/∂u∂v+a ∂2z/∂v2,∂2 z...
查看完整答案讨论
计算曲面积分∬S(2x+z)dydz+zdxdy，其中S为有向曲面z=x2+y2 (0≤z≤1)，其法向量与z轴正向的夹角为锐角.
设x1=10,xn+1=(n=1,2,⋯)，试证数列{xn}的极限存在，并求此极限.
设f(x)有连续的导数，f(0)=0,f'(0)≠0,F(x)=(x2-t2) f(t)dt，且当x→0时，F'(x)与xk是同阶无穷小，则k等于【 】
设an>0(n=1,2,⋯)，且an 收敛，常数λ∈(0,π/2)，则级数(-1)n (ntan λ/n) a2n【 】
设f(x)有二阶连续导数，且f' (0)=0,f''(x)/|x|=1，则【 】
已知((x+ay)dx+ydy)/(x+y)2 为某函数的全微分，则a等于【 】
设ξ,η是两个相互独立且均服从正态分布N(0,1/2)的随机变量，则随机变量|ξ-η|的数学期望E(|ξ-η|)=________.
设工厂A 和工厂B的产品的次品率分别为1% 和 2%，现从由 A 厂和 B厂的产品分别占60% 和 40% 的一批产品中随机抽取一件，发现是次品，则该次品属 A厂生产的概率是________.
设z=1/x·f(xy)+yf(x+y)，求∂2z)/∂x∂y.
若f(x,y)的偏导数fx,fy在(x0,y0)存在，则f(x,y)在(x0,y0)连续.
用变换ξ=x,η=x2+y2化简方程y ∂z/∂x-x ∂z/∂y=0，并求出这个方程的通解z=z(x,y).
二元函数f(x,y)在点(x0,y0)处两个偏导数fx' (x0,y0 ),fy' (x0,y0)存在是f(x,y)在该点连续的【 】
设φ(t),ψ(t)有二阶连续导数，u=φ(y/x)+xψ(y/x)，求：x2 ∂2u/∂x2+2xy ∂2u)/∂x∂y+y2 ∂2u/∂y2.
设u=e-xsin(x/y)，则∂2u)/∂x∂y在点(2,1/π)处的值为________.
已知：z=x2 F(y/x2)，其中F(u)的一阶偏导数存在，证明：x ∂z/∂x+2y ∂z/∂y=2z.
已知z=f(u,v)，其中u=2x+y,v=x2，求∂z/∂x,∂z/∂y,∂2/∂x2,∂2z/∂x∂y.
函数u=ln(x2+y2+z2)在点M(1,2,-2)处的梯度 gradu|M=__________.
在曲线x=t,y=-t2,z=t3的所有切线中，与平面x+2y+z=4平行的切线是【 】
由曲线绕y轴旋转一周得到的旋转柱面在点(0,√3,√2)处的指向外侧的单位法向量为__________.
曲面z-ez+2xy=3在点(1,2,0)处的切平面方程为____________.
函数u=ln(x+)在A(1,0,1)处沿A点指向B(3,-2,2)点方向的方向导数为________.
设函数f(x,y)可微，且f(x+1,ex)=x(x+1)2 , f(x,x2)=2x2lnx，则df(1,1)=【 】
已知f(x,y)在(x0,y0)的某邻域内，fx(x,y)连续，fy(x0,y0)存在，证明：f(x,y)在(x0,y0)可微.