设数列{xn}为x1=1，xn+1=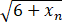 
(n=1,2,…)，求证数列{xn}收敛，并求其极限.
-
关注优题吧，注册平台账号.
题吧，智能辅助学习中心
证明题（2008年江苏省）
答案解析
因为x2= = >1=x1，且归纳假设0<xn-1<xn ⇒ 0<6+xn-1<6+xn ⇒ xn= < = xn+1，所以数列{xn}单调递增。又x1 < ...
查看完整答案讨论
已知φ(x)=|x-t|f(t)dt，若积分存在，且f(x)>0，证明：φ(x)为[a,b]上的凸函数.
当x→0时，函数f(x)=ax+bx2+ln(1+x)与g(x)=ex^2 -cosx是等价无穷小，则ab=______.
已知{xn },{yn}满足x1=yn=1/2,xn+1=sinxn,yn+1=yn2 (n=1,2,⋯) ，则当n→∞时【 】
当x→0时，用“o(x)”表示比x高阶的无穷小，则下列式子中错误的是【 】
已知函数f(x)是周期为π的奇函数，且当x∈（0，π/2）时f(x)=sinx-cosx+2，则当x∈（π，π/2）时f(x)=____________________.
函数y=sinx|sinx|（其中|x|≤π/2）的反函数为____________________.
设函数f(x)在[a,b]上有定义，在(a,b)上连续.下面哪个条件能够判定函数f(x)在[a,b]上有最大值【 】
在平面直角坐标系中，椭圆x2+xy+y2=1的长轴方程为__________，位于x轴上半平面内的焦点坐标为__________.