计算曲面积分I=∬Σ(x3+az2)dydz+(y3+ax2)dzdx+(z3+ay2)dxdy,其中Σ为上半球面z=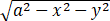 的上侧.
的上侧.
计算题(1992年理工数学Ⅰ)
答案解析
令Σ1表示 ,其法向量与z轴负向相同,Ω表示Σ与Σ1所围成的闭区域,有I=∬Σ+Σ1(x3+az2 )dydz+(y3+ax2 )dzdx+(z3+ay2)dxdy -∬Σ1(x3+az2 )dydz+(y3+ax2 )dzdx+(z3+ay2)dxdy,由高斯公式得∬Σ+Σ1(x3+az2 )dydz+(y3+ax2 )dzdx+(z3+ay2)dxdy =∭Ω3(x2+y2+z...
查看完整答案讨论
求曲面积分∬S(z3-x)dydz-xydzdx-3zdxdy.其中S是由曲面z=4-y2,平面x=0,平面x=3以及xOy平面围成立体的表面,取外侧.
计算曲面积分∬S(2x+z)dydz+zdxdy,其中S为有向曲面z=x2+y2 (0≤z≤1),其法向量与z轴正向的夹角为锐角.
计算∯Σ 2zxdydz+yzdzdx-z2 dxdy,其中Σ是由曲面z=与z=所围成的表面外侧.
设半径为R的球面Σ的球心在定球面x2+y2+z2=a2 (a>0)上,问当R为何值时,球面Σ在定球面内部的那部分的面积最大?
已知向量组α1=(1,2,3,4),α2=(2,3,4,5),α3=(3,4,5,6),α4=(4,5,6,7),则该向量组的秩是______.
已知函数f(x)具有任意阶导数,且f' (x)=[f(x)]2,则当n为大于2的正整数时,f(x)的n阶导数f(n) (x)等于【 】
已知f(x)在x=0的某个领域内连续,且f(0)=0,f(x)/(1-cosx)=2,则在点x=0处f(x)【 】
计算第二型曲面积分x(x2+1)dydz+y(y2+2)dzdx+z(z2+3)dxdy其中Σ为球面x2+y2+z2=1的外侧.
设Σ为空间区域{(x,y,z)|x2 + 4y2≤4,0≤z≤2}表面的外侧,则曲面积分∬Σx2dydz + y2dzdx + z2dxdy=______.
f(x)满足∫f(x)/dx = 1/6·x2 - x + C,L为曲线y=f(x)(4≤x≤9),L的弧长为s,L绕x轴旋转一周所形成的曲面的面积为A,求s和A.
计算第二型曲面积分∬S,其中S是下半球面z=-的下侧,a>0是常数.
设S是x2+y2+z2=1的外侧,计算∬Sx(x2+1)dydz+y(y2+2)dzdx+z(z2+3)dxdy
曲线(x2 + y2)2 = x2 - y2 (x≥0,y≥0)与x轴围成的区域为D,求xydxdy.
设有界区域D是圆x2 + y2 = 1和直线y=x以及x轴在第一象限围成的部分,计算二重积分(x2 - y2)dxdy.
设D由y=sinπx(0≤x≤1)与x轴转成,则D绕x旋转的旋转体体积为__________.
设F=yz(2x+y+z)i+xz(x+2y+z)j+xy(x+y+2z)k.求:F沿螺线r=acost∙i+asint∙j+bt∙k的一段(t:0→π/4)所作的功.
计算曲面积分I=∬∑x(8y+1)dydz+2(1-y2 )dxdz-4yzdxdy,其中∑是由曲线(1≤y≤3)绕y轴旋转一周而成的曲面,其法向量与y轴正向的夹角恒大于π/2.
已知曲线L的极坐标方程为r=sin3θ(0≤θ≤π/3),则L围成有界区域的面积为__________.
设Γ是上半球面x2+y2+z2=R2 (z≥0)上的光滑曲线,起点和终点分别在平面z=0,z=R/2上,曲线的切线与z轴正方向的夹角为常数α∈(0,π/6),求曲线Γ的长度.

