求第二类曲线积分∫Ly/(x2+y2)dx-x/(x2+y2)dy,其中L为椭圆x2+1+4y2-4x=0,方向为逆时针.
计算∫Lxdy-ydx,其中L:x2+y2=1,取逆时针方向.
若函数f(x)在[a,b]上连续(b>0),在(a,b)内可导,且f(a)=0,证明:存在ξ∈(a,b),使得f'(ξ)=ξf(ξ)/(b-ξ).
求椭圆x2/4+y2=1到直线x+2y-3=0的距离的最小值.
求第二类曲线积分∫Ly/(x2+y2)dx-x/(x2+y2)dy,其中L为椭圆x2+1+4y2-4x=0,方向为逆时针.
求第二类曲线积分∫Ly/(x2+y2)dx-x/(x2+y2)dy,其中L为椭圆x2+1+4y2-4x=0,方向为逆时针.
求第二类曲线积分∫Ly/(x2+y2)dx-x/(x2+y2)dy,其中L为椭圆x2+1+4y2-4x=0,方向为逆时针.
求第二类曲线积分∫Ly/(x2+y2)dx-x/(x2+y2)dy,其中L为椭圆x2+1+4y2-4x=0,方向为逆时针.
计算积分∬SzdS,其中S为曲面x2+z2=2az(a>0)被曲面z=所截的部分.
设D⊂R2是有界单连通闭区域,I(D)=(4-x2-y2)dxdy取得最大值的积分区域记为D1.(1) 求I(D1 )的值.(2) 计算,其中∂D1是D1的正向边界.
设Γ是上半球面x2+y2+z2=R2 (z≥0)上的光滑曲线,起点和终点分别在平面z=0,z=R/2上,曲线的切线与z轴正方向的夹角为常数α∈(0,π/6),求曲线Γ的长度.
设F=yz(2x+y+z)i+xz(x+2y+z)j+xy(x+y+2z)k.求:F沿螺线r=acost∙i+asint∙j+bt∙k的一段(t:0→π/4)所作的功.
设L为取正向的圆周x2+y2=9,则曲线积分∮L(2xy-2y)dx+(x2 - 4x)dy=________.
计算曲面积分I=∬∑x(8y+1)dydz+2(1-y2 )dxdz-4yzdxdy,其中∑是由曲线(1≤y≤3)绕y轴旋转一周而成的曲面,其法向量与y轴正向的夹角恒大于π/2.


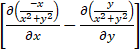 dxdy=∬D0dxdy=0.
dxdy=∬D0dxdy=0.