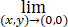xy (3x-4y)/(x2+y2)
-
关注优题吧，注册平台账号.
题吧，智能辅助学习中心
计算题（2022年同济大学）
答案解析
令x=rcosθ,y=rsinθ，
则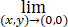
xy (3x-4y)/(x2+y2)=
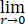rsinθcosθ(3cosθ-4sinθ)=0.
讨论
计算∬Ωe(x-y)/(x+y) dΩ，其中Ω:x≥0,y≥0,x+y≤1.
设f(x)在(0,1)可微，且有x2 f(x) dx=0，证明：存在θ∈(0,1)，使得f' (θ)=-f(θ)/θ.
计算 ∬∑x3dydz，其中∑: x2/a2 +y2/b2 +z2/c2 =1,z≥0，取外侧.
计算(e-ax - e-bx)/x sinxdx，其中a,b>0.
设f(x,y)=，问：f(x,y)在(0,0)处连续吗？方向可导吗？可微吗？
已知an=+∞，证明(a1+a2+⋯+an)/n=+∞，并举例说明反过来不成立.
已知函数f(x)在[a,+∞)上连续，且f(x)存在，证明：(1)函数f(x)有界；(2)存在ξ∈[a,+∞)，使得f(ξ)为f(x)在[a,+∞)上的最大值或最小值.
设z=f(ex siny,x2+y2)，其中f具有二阶连续偏导数，求∂2z/∂x∂y.
由曲线绕y轴旋转一周得到的旋转柱面在点(0,√3,√2)处的指向外侧的单位法向量为__________.
曲面z-ez+2xy=3在点(1,2,0)处的切平面方程为____________.
设直线l:在平面π上，且平面π与曲面z=x2+y2相切于点(1,-2,5)，求a,b的值.
已知((x+ay)dx+ydy)/(x+y)2 为某函数的全微分，则a等于【 】
设函数f(u)具有二阶连续导数，而z=f(exsiny)满足方程∂2z/∂x2+∂2z/∂y2=e2x z,求f(u).
设z=1/x f(xy)+yφ(x+y),f,φ具有二阶连续导数，则∂2z/∂x∂y=________________.
设x(y),z(y)是由方程组所确定的隐函数，求x'(y),z'(y).
设参数方程x=f'(t),y=tf'(t)-f(t)，其中函数f(t)可以求导足够次数，求一阶导数dy/dx和二阶导数d2y/dx2.