大学数学-考研试题(浙江大学 2024年数列收敛的性质)

问答题（2024年浙江大学）

设x₁=1,x_n+1=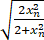,n=1,2,3,⋯

(1)证明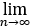：x_n =0.

(2)计算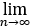n(x_n-ln⁡(1+x_n)).

答案解析

暂无答案

讨论

数列收敛的性质

已知正项级数an 收敛，数列{xn}满足|xn+1-xn |≤a_n,∀n≥1.证明：{xn}收敛.

设fn (x)在(a,b)上单调递增，且有实数列{Mn },n=1,2,3,…使得∀x∈(a,b),|fn (x)|≤Mn，若fn (x)在(a,b)上一致收敛于f(x)，证明：(1)存在M>0，使得∀x∈(a,b),|f(x)|≤M;(2)极限f(x)存在.

由下面哪个条件能够判断{xn}收敛【】

假设5/11是整系数多项式f(x)的根，证明：f(√(-1))f(-√(-1))是正整数，且是146的倍数.

求线性方程组的基础解系，假设该方程组的一个解和另外一个解为k1+k2 的方程组有公共解，求出所有公共解.

设X=(x1,x2,x3,x4 ),XT是X的转置，问是否存在一次多项式ui (x)=ai x1+bi x2+ci x3+di x4 (i=1,2,3,4)满足XXT=并说明理由.

假设R是实数域，实向量空间R³中两组向量分别为α1=(-1,1,0),α2=(2,-1,2),α3=(0,1,b)和β1=(1,0,-1),β2=(-1,1,1),β3=(1,1,c).(1)当b,c取何值时，不存在R³上的线性变换F，满F(αi )=βi,i=1,2,3.(2)当b,c取何值时，至少存在两个R³上的线性变换F，满足F(αi )=βi,i=1,2,3.(3)当b,c取何值时，存在R³上的唯一线性变换F，满足F(αi )=βi,i=1,2,3.这样的线性变换是正交变换吗？为什么？

假设A是2024阶方阵，主对角线上全是偶数，其余的都是奇数.证明：该矩阵为可逆矩阵.

求f(x)=x4+2x³-x²-4x-2,g(x)=x4+x³-x²-2x-2的最大公因式d(x)以及多项式u(x),v(x)，满足d(x)=u(x)f(x)+v(x)g(x).

已知矩阵A=的特征值λ对应的特征向量α=，求该矩阵的若当(Jordan)标准型.

数列极限

求(1²+3²+⋯+(2n-1)²)/n³

设数列{xn}满足xmn≤xm+xn,xn>0，证明：存在.

浙江大学数列极限

设函数f,g在[0,1]上连续，且存在包含于[0,1] 的数列{xn}，使得对于任意n≥1，有f(xn)= g(xn+1).证明：存在ξ∈[0,1],使得 f(ξ)=g(ξ).

((n-2)/(n+1))n=________.

求⁡[sin⁡(π/n)/(n+1)+sin(2π/n)/(n+1/2)+⋯+sinπ/(n+1/n)]

(1+22√2+32∛3+⋯+n2)/n3

设an=a,且a≠0，则当n充分大时，有【】.

设{an}，{bn}，{cn}均为非负数列，且an=0， bn=1，cn=∞，则必有【】

对有界数列{xn}，下面哪个说法可作为xn=L的定义【】（此题不全，待更新）

函数与极限

当x→0+时，下列无穷小阶数最高的是【】

(1/(ex-1)-1/ln⁡(1+x) )=______.

东北师范大学两个重要极限

设y=y(x)由方程y²-x+siny=0(x≥1)确定，且y=y(x)经过(π²,π).试讨论y(x)在(1,+∞)上零点的个数，并求y(x).

设f(x)在[a,b)上严格单调，xn∈(a,b)，证明：如果f(xn)=f(a)，则xn=a.

设f(x),g(x)在(-∞,+∞)上连续，且[f(x)-g(x)]=0.证明：f(x)在(-∞,+∞)上一致连续当且仅当g(x)在(-∞,+∞)上一致连续.

函数f(x)=|x|1/(1-x)(x-2)的第一类间断点的个数是【】

若((1+ax²)sinx-1)/x³=6，则a=______.

设函数f(x)=(1+x)/(1+nx2n)，则f(x)【】

当x→0时，((1+t²)sint²)/(1+cost²) dt与xk是等阶无穷小，则k=______.