设f(x)=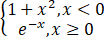 ,求
,求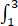 f(x-2)dx.
f(x-2)dx.
计算题(1992年理工数学Ⅰ)
答案解析
令x-2=t,则dx=dt,当x=1时,t=-1;当x=3时,t=1,于是
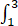 f(x-2)dx=
f(x-2)dx=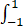 f(t)dt=
f(t)dt=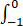 (1+t2)dt+
(1+t2)dt+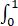 e-tdt
e-tdt
= (t+1/3 t3 )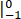 - e-t
- e-t 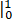 =7/3-1/e.
=7/3-1/e.
讨论
设f(x)在(-∞,+∞)内连续可导,且m≤f(x)≤M,a>0.(1)求1/(4a2)[f(t+a)-f(t-a)]dt;(2)求证:|1/2af(t)dt-f(x)|≤M-m.
将长为a的铁丝切成两段,一段围成正方形,另一段围成圆,问这两段铁丝长各为多少时,正方形与圆的面积之和为最小?
作函数y=6/(x2-2x+4),并填写表.单调增加区间:单调减少区间:极值点:极值:凹区间:凸区间:拐点:渐近线:
求微分方程y'+1/x y=1/(x(x2+1))的通解(一般解).
由曲线y=sin3/2x (0≤x≤π)与x轴围成的平面绕x轴旋转而的旋转体的体积为【 】
若y=f(x),有f'(x0)=1/2,则当∆x→0时,该函数在x=x0处的微分dy是【 】
设f(x)是连续函数,且f(x)=x+2f(t)dt=________.
积分中值定理的条件是__________,结论是____________.
设f(x)是连续函数,且F(x)=f(t)dt,则F'(x)等于【 】
设函数f(x)在[0,1]上连续,在(0,1)内可导,且3f(x)dx=f(0),证明:在(0,1)内存在一点c,使f'(c)=0.
设f(x)连续,且f(t)dt=x,则f(7)=__________.
证明:xasinxdx∙a-cosx dx≥π³/4其中,a>0为常数.
设f(a)=0,f(x)在[a,b]上的导数连续,求证:1/(b-a)²·|f(x)|dx≤1/2 maxx∈[a,b] |f'(x)|,x∈[a,b]

