大学数学-考研试题(理工数学Ⅱ 1989年定积分的换元法)

计算题（1989年理工数学Ⅱ）

已知f(2)=1/2,f'(2)=0及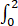f(x)dx=1，求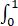x²f''(2x)dx.

答案解析

令t=2x,则dx=1/2 dt，当x=0时, t=0，当x=1时，t=2，于是x2 f'' (2x) dx=1/4 t2 f'' (t)∙1/2 dt=1/8 t2 d[f' (t)] =1/8 ...

查看完整答案

讨论

定积分的分部积分法

设函数f(x)在开区间[0,1]上可微，f(0)=0，且在[0,1]内0<f'(x)<1，证明：(1)对于任意x∈(0,1),f(t)dt>1/2 f2 (x);(2) (f(x)dx)2>f3(x)dx.

求ln⁡(1+x)/(2-x)2 dx.

求ln⁡(1+x)/(2-x)2 dx.

tsint dt=__________.

利用留数定理计算下列积分cos(bx)dx（a>0,b为实数）

利用δ函数的性质，计算积分δ(x2+1)sinxdx.

求定积分sinθ/(sinθ+cosθ) dθ.

计算积分xm-1/(1+xn) dx，其中0<m<n.

∫f'(x)dx=__________.

定积分的换元法

e√x =__________.

设f(x)=，求f(x-2)dx.

证明：sin⁡(x²)dx>0.

浙江省定积分的换元法

利用δ函数计算下列积分(x2+1)δ(x2-2x-8)dx.

若f(x)为已知连续函数，I=tf(tx)dx，其中t>0,s>0，则I的值【】

求定积分x(sinx)arctan⁡(e-x)/(1+cos2⁡x )dx

设连续函数f(x)满足f(x+2)-f(x)=x,f(x)dx=0，则f(x)dx=______.

设x,t>0，则含参变量积分I(t)=(e-x -e-xt)/x dx=________.

定积分

f'(2x)dx=__________.

设f(x)是连续函数，且F(x)=f(t)dt，则F'(x)等于【】

设函数f(x)在[0,1]上连续，在(0,1)内可导，且3f(x)dx=f(0)，证明：在(0,1)内存在一点c，使f'(c)=0.

设f(x)连续，且f(t)dt=x，则f(7)=__________.

设f(x)在(-∞,+∞)内连续可导，且m≤f(x)≤M,a>0.(1)求1/(4a2)[f(t+a)-f(t-a)]dt;(2)求证：|1/2af(t)dt-f(x)|≤M-m.

设M=sinx/(1+x2)cos4⁡x dx,N=(sin3x+cos4⁡x )dx,P=(x2sin3⁡x-cos4⁡x)dx，则有【】

d/dx xcost2dt=______________.

证明：xasinxdx∙a-cosx dx≥π³/4其中，a>0为常数.

设f(a)=0,f(x)在[a,b]上的导数连续，求证：1/(b-a)²·|f(x)|dx≤1/2 maxx∈[a,b] ⁡|f'(x)|,x∈[a,b]