求级数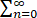
(-1)n(n2-n+1)/2n 的和.
-
关注优题吧，注册平台账号.
题吧，智能辅助学习中心
计算题（1993年理工数学Ⅰ）
答案解析
几何级数(-1/2)n =1/(1-(-1/2))=2/3,令S(x)=n(n-1) xn-2 ，有S(x)=n(n-1) xn-2 =(nxn-1 )'=(xn )'' =(x/(1-x))''=2/(1-x)3 ...
查看完整答案讨论
计算∯Σ 2zxdydz+yzdzdx-z2 dxdy，其中Σ是由曲面z=与z=所围成的表面外侧.
求微分方程x2y'+xy=y2满足初始条件y|x=1=1的特解.
设曲线积分∫L[f(x)-ex]sinydx-f(x)cosydy与路径无关，共中f(x)具有一阶连续导数，且f(0)=0，则f(x)等于【 】
设直线l1:(x-1)/1=(y-5)/(-2)=(z+8)/1与l2:则l1与l2的夹角为【 】
双纽线(x2+y2)2=x2-y2所围成的区域面积可用定积分表示为【 】
设f(x)=sint2dt,g(x)=x3+x4，则当x→0时，f(x)是g(x)的【 】
设随机变量X服从(0,2)上的均匀分布，则随机变量Y=X2在(0,4)内的概率分布密度fY(y)=__________.
求幂级数(3+(-1)n)n/n xn的收敛半径，并判断它在收敛区间端点的收敛情况.
证明：(1)级数 sin(2nπx)/2n 在区间(-∞,+∞)上连续；(2)函数f(x)=sin(2nπx)/2n 在任何区间上不能逐次求导.
设幂级数an(x-1)n在x=-1处收敛，则此级数在x=2处【 】
已知幂级数(-1)nn(n+1) xn .(1)求幂级数的收敛半径、收敛区间以及和函数；(2)计算(-1)nn(n+1)/4n .
幂级数n/(2n+(-3)n) x2n-1的收敛半径R=________.
求幂级数((-4)n+1)/(4n (2n+1)) x2n 的收敛域及和函数S(x).
在过点O(0,0)和A(π,0)的曲线族y=asinx(a>0)中，求一条曲线L，使沿该曲线从O到A的积分∫L(1+y3) dx+(2x+y)dy的值最小.
将函数f(x)=2+|x|(-1≤x≤1)展开成以2为周期的傅里叶级数，并由此求级数1/n2 的和.
设f(x)=，则其以2π为周期的傅里叶级数在点x=π处收敛于__________.
设函数f(x)=πx+x2 (-π<x<π)的傅里叶级数展开式为a0/2+(ancosnx+bnsinnx)，其中系数b3的值为__________.
设un(x) = e-nx + xn+1 (n=1,2,…)，求级数un(x)的收敛域和函数.
设n为正整数，y=yn (x)是微分方程xy' - (n+1)y=0满足条件yn(1)=1/n(n+1)的解.(1) 求yn (x);(2) 求级数yn(x)的收敛域及和函数.