设向量α1=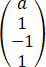 ,α2=
,α2=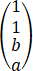 ,α3=
,α3=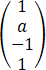 ,若α1,α2,α3线性相关,且其中任意两个向量均线性无关,则【 】
,若α1,α2,α3线性相关,且其中任意两个向量均线性无关,则【 】
A、a=1,b≠-1
B、a=1,b=-1
C、a≠-2,b=2
D、a=-2,b=2
设向量α1=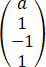 ,α2=
,α2=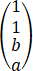 ,α3=
,α3=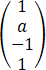 ,若α1,α2,α3线性相关,且其中任意两个向量均线性无关,则【 】
,若α1,α2,α3线性相关,且其中任意两个向量均线性无关,则【 】
A、a=1,b≠-1
B、a=1,b=-1
C、a≠-2,b=2
D、a=-2,b=2
D
【解析】
解答过程见word版
设V是欧氏空间,W是V的子空间,V中的向量α不在W中,问是否存在α0∈W,使得α-α0与W的任意向量都正交?如果不存在,举出例子;如果存在,说明理由并讨论其唯一性.
设R2中的内积为(α,β)=α' Aβ,A=,则,在此内积之下的度量矩阵为________.
已知同维数的两个向量组有相同的秩,且其中之一可用另外一个线性表示,证明:这两个向量组等价。
设向量组A:α1,α2,… ,αs可以由向量组B:β1,β2,… ,βt线性表示且R(A)=R(B).证明向量组A与向量组B等价.
设xoy在平面上n个结点Mi(xi,yi ),i=1,2,…,n(n≥3).证明:M1,M2,…,Mn在同一条直线上⟺R=2.
已知三维向量空间的基底为α1=(1,1,0)T,α2=(1,0,1)T,α3=(0,1,1)T,则向量β=(2,0,0)T在此基底下的坐标是____________.