定义在全体实数上的连续函数f(x)满足下列条件:
当n-1≤x<n时,|f(x)|=|6(x-n+1)(x-n)|( n正整数)
定义在开区间(0,4)上的函数g(x)=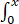 f(t)dt-
f(t)dt-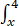 f(t)dt.若g(x)在x=2处取得最小值0,则
f(t)dt.若g(x)在x=2处取得最小值0,则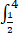 f(x)dx的值为【 】
f(x)dx的值为【 】
A、-3/2
B、-1/2
C、1/2
D、3/2
E、5/2
定义在全体实数上的连续函数f(x)满足下列条件:
当n-1≤x<n时,|f(x)|=|6(x-n+1)(x-n)|( n正整数)
定义在开区间(0,4)上的函数g(x)=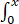 f(t)dt-
f(t)dt-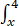 f(t)dt.若g(x)在x=2处取得最小值0,则
f(t)dt.若g(x)在x=2处取得最小值0,则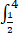 f(x)dx的值为【 】
f(x)dx的值为【 】
A、-3/2
B、-1/2
C、1/2
D、3/2
E、5/2
暂无答案
如图所示,四边形ABCD内接于圆,(AB) ̅=5,(AC) ̅=3√5,(AD) ̅=7,∠BAC=∠CAD,则圆的半径为【 】
记曲线y=x3+x2,y=-x2+k(4<k<5)与y轴围成的面积为A,这两条曲线与直线x=2围成的面积为B,如图所示,若A=B,则k的值为【 】
函数f(x)=a-√3tan2x在闭区间[-π/6,b]上的最大值为7,最小值为3,则a×b的值为【 】
过点(0,4)作曲线y=x3-x+2的切线,这条切线在x轴上的截距为【 】
等差数列{an}的各项均为正数,首项与公差相等,=2,则a4的值为【 】
已知函数f(x)=2x3-9x2+ax+5在x=1处取得极大值,在x=b处取得极小值,则a+b的值为【 】
已知tanθ<0,cos(π/2+θ)=√5/5,则cosθ的值为【 】
设f(x)为多项式函数,g(x)=x2 f(x),若f(2)=1,f'(2)=3,则g'(2)的值为【 】
利用积分计算椭圆x2/a2 +y2/b2 =1(a>b>0)所围成的面积.
不大于log2(x3+1)dx+(2x-1)1/3dx的最大整数是______.
关于方程(lnx)1/2/(x[a-(lnx)1/2]2) dx=1,α∈(-∞,0)∪(1,+∞),下列叙述正确的有【 】
对于一个实数x,令{x}=x-[x]. 记S=min({x/8},{x/4}) dx,则[S]=______.
对于函数f(x),已知f'(x)=4x3-2x,且f(0)=3,求f(2)的值.
Find the area bounded by the curves.y = sinx of y = 1/2sinx between x = 0 and x = π.