高中数学-高考试题(全国旧课程 2003年三角函数及性质)

单项选择（2003年全国旧课程）

已知x∈(-π/2,0),cosx=4/5，则tan2x=【】

A、7/24

B、-7/24

C、24/7

D、-24/7

答案解析

D

【解析】

∵x∈(-π/2,0),cosx=4/5,

∴sinx=-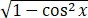=-3/5,tanx=sinx/cosx=-3/4,

∴tan2x=2tanx/(1-tan²⁡x )=-24/7.

讨论

高中数学

Let n be a positive integer. A“Northern European Square Matrix (NESM) is an n×n square containing all the integers from 1 to n²,so that there is exactly one number in each grid.The two different grids are neighbours if they share a common edge.A grid is called a "valley”if the integer in it in smaller than the integers in all the neighbours of the grid. An "uphill path”is a sequence containing one or more grids satisfying:(i)the frist grid of the sequence is a valley,(ii) each subsequent grid in the sequence is the neighbour of its previous grid,(iii) the integers in the girds of the sequence is incremented.Figure out the minimum possible value of the number of uphill paths in a NESM which should be represented by a function of n.译文：令n为一个正整数，一个“北欧方阵”是一个包含1至n²所有整数的n×n的方格表，使得每个方格中恰有一个数字。两个相异方格如果有公共边，称它们是相邻的。如果一个方格内的数字比所有相邻方格内的数字都小，称其为“山谷”。一条“上坡路径”是一个包含一或多个方格的序列，满足：(1)序列的第一个方格是山谷；(2)序列中随后的每个方格都和前一个方格相邻；(3)序列中方格所写的数字递增。试求一个北欧方阵中山坡路径的最小可能值，以n的函数表示之。

Find all the groups of positive integers (a,b,p) satisfying p is a prime number and ap=b!+p.译文：求所有正整数组(a,b,p)，满足：p为素数且ap=b!+p.

Suppose a convex pentagon ABCDE such that BC=DE.If there exists a point T inside ABCDE suchthat TB=TD TC=TE and ∠ABT=∠TEA. AB meet CD and CT at point P and Q respectively, withP,B,A,Q in this order on the same line. AE meet CD and DT at point R and S respectively, with R,E,A,S in this order on the same line.Prove that P,S,Q,R are on the same circle.译文：设凸五边形ABCDE满足BC=DE.若在ABCDE内存在一点T使得TB=TD,TC=TE且∠ABT= ∠TEA.直线AB分别与直线CD和CT交于点P和Q，且P,B,A,Q在同一直线上按此顺序排列;直线AE分别与直线CD和DT交于点R和S，且R,E,A,S在同一直线上按此顺序排列.证明：P,S,Q,R 四点共圆.

Let k be a positive integer and let S be a finite set of odd prime numbers. Prove that there is at most one way (up to rotation and refection) to place the elements of S around a circle such that the product of any two neighbours is of the form x2+x+k for some positive integer x. 译文：给定正整数 k,S是一个由有限个奇素数构成的集合.证明：至多只有一种方式(旋转或对称后相同视为同种方式)可以将S中的元素排成一个圆周，且满足任意两个相邻元素的乘积均可以写成x2+x+k的形式 (其中x为正整数) .

Let R+ denote the set of positive real numbers. Find all functions f:R⟶R such that for each x∈R+, there is exactly one y∈R+ satisfying：xf(y)+yf(x)≤2.译文：设R+表示所有正实数构成的集合.求所有函数f:R+→R+，使得对任意x∈R+，恰好有一个y∈R+满足条件：xf(y)+yf(x)≤2.

The Bank of Oslo issues two types of coin：aluminium(denoted A) and bronze(denoted B). Marianne has n aluminium coins and n bronze coins, arranged in a row in some arbitrary initial order.A chain is any subsequence of consecutive coins of the same type.Given a fixed positive integer k<2n, Marianne repeatedly performs the following operation：she identifies the longest chain containing the kth coin from the left and moves all coins in that chain to the left end of the row.For example, if n = 4 and k=4 the process starting from the ordering AABBBABA would beAABBBABA→BBBAAABA→AAABBBBA→BBBBAAAA.Find all pairs (n, k) with 1 ≤ k ≤2n such that for every initial ordering at some moment during the process,the leftmost n coins will all be of the same type. 译文：奥斯陆银行发行了两种货币：铝币(记为A)和铜币(记为B).玛丽安有n枚铝币和n枚铜币，以任意初始方式排成一排。定义一条链为任意由相同类型货币构成的连续子列。给定正整数k<2n，玛丽安重复地进行如下操作：她找出包含(从左到右)第k枚硬币的最长链，然后把该链中所有货币移到序列最左端。例如，n=4，k=4时，对于初始序列 AABBBABA，过程如下：AABBBABA→BBBAAABA→AAABBBBA→BBBBAAAA.求所有满足1≤k≤2n的数组(n，k)，使得对任意初始序列，都可以在有限次操作内使左端为n枚相同的货币。

数列{an}中，a1=1,a2=3，若地任意n(n≥2)都存在正整数i(1≤i≤n-1)使得an+1=2an-ai.(1)求a4的所有可能值.(2)命题p：若a1,a2,a3,…,a8成等差数列，则a9<30，证明命题p为真；写出p的逆命题q，并判断q的真假，若命题q为真则证明，若命题q为假，请举出反例.(3)若对任意正整数m,a2m=3m，求数列{an}的通项公式.

已知Γ:x2/a2 +y2/b2 =1(a>b>0)的左、右焦点分别为F1 (-√2,0),F2 (√2,0),A为Γ的下顶点，M为直线l:x+y-4√2=0上一点.(1)若a=2,AM的中点在x轴上，求点M的坐标；(2)直线l交y轴于点B，直线AM经过点F2，若△ABM有一个内角的余弦值为3/5，求b；(3)若椭圆Γ上存在点P到直线l的距离为d，且满足d+|PF1 |+|PF2 |=6，当a变化时，求d的最小值.

如图，AD=BC=6，AB=20，∠ABC=∠DAB=120°，O为AB中点，曲线CMD上所有的点到O的距离相等，MO⊥AB，P为曲线CM上的一动点，点Q与点P关于OM对称.(1)若P在点C的位置，求∠POB的大小; (2)求五边形MQABP面积的最大值.

已知f(x)=log3(x+a)+log3(6-x).若将函数y=f(x)的图像向下平移m(m>0)个单位，经过点(3,0),(5,0)，求a与m的值；若a>-3且a≠0，解关于x的不等式f(x)≤f(6-x).

三角函数

cos2 π/12 - cos2 5π/12=【】

求证：(sinα+sinβ)/sin⁡(α+β)=cos((α-β)/2)/cos((α+β)/2)

解方程：sinx+cosx-1=0

计算：sin 4π/3∙cos 25π/6∙tg(-3π/4).

已知x+x-1=2cosθ，求证：xn+x-n=2cosnθ.

不查表求sin105°的值.

设函数f(x)=sin⁡(ωx+π/3)在区间(0,π)恰有三个极值点、两个零点，则ω的取值范围是【】

记△ABC的内角A,B,C的对边分别为a,b,c，已知sin⁡Csin⁡( A-B)=sin⁡Bsin⁡(C-A)．（1）证明：2a2=b2+c2；（2）若a=5,cos⁡A=25/31，求△ABC的周长．

函数f(x)=cos⁡x+(x+1)sin⁡x+1在区间[0,2π]的最小值、最大值分别为【】

为了得到函数y=2sin⁡3x的图像，只要把函数y=2sin⁡(3x+π/5)图像上所有的点【】

三角函数及性质

若sinθcosθ>0，则θ在【】

求函数y=(sinx+cosx)2+2cos2x的最小正周期.

下列区间中，函数f(x)=7sin⁡(x-π/6)单调递增的区间是【】

函数f(x)=sin x/3+cos x/3的最小正周期和最大值分别是【】

已知函数f(x)=cosx-cos2x，则该函数【】

已知f(x)=3sinx+2，对任意的x1∈[0,π/2]，都存在x2∈[0,π/2]，使得f(x1)=2f(x2+θ)+2成立，则下列选中θ可能的值是【】

(tg(-120°)∙cos⁡(-240°)∙cos480°)/(tg(-60°)∙sin⁡(-105°))

设f(x)=sin4⁡x-sinxcosx+cos4⁡x，则f(x)的值域是__________________.

已知函数f(x)=sin⁡(ωx+φ)，如图A,B是直线y=1/2与曲线y=f(x)的两个交点，若|AB|=π/6，则f(π)=________.

已知函数 f(x)=sin⁡(x+π/3). 给出下列结论:① f(x) 的最小正周期为 2π;② f(π/2) 是 f(x) 的最大值;③ 把函数 y = sin x 的图像上所有点向左平移 π/3个单位长度, 可得到函数 y = f(x) 的图像.其中所有正确结论的序号是【】.