设坐标原点为O，抛物线y2=2x与过焦点的直线交于A,B两点，则
∙
=【 】
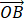A、3/4
B、-3/4
C、3
D、-3
-
关注优题吧，注册平台账号.
题吧，智能辅助学习中心
从点(-8,8)引 2xy +y² =8 的两条切线，求它们的夹角.
若相相之二抛物线具有相同之顶点，且其主轴互相垂直，试证其公切线必与二抛物线各切于其通径之一端.
设 F 是抛物线的焦点，在抛物线上任取一点 P 与焦点连接，由 P 作 PQ平于主轴，试证 P 点的法线平分 ∠FPQ.
在直角坐标系xOy中，点P到x轴的距离等于点P到点(0,1/2)的距离，记动点P的轨迹为W.(1)求W的方程；(2)已知矩形ABCD有三个顶点在W上，证明：矩形ABCD的周长大于3√3.
设O为坐标原点，直线y=-√3(x-1)过抛物线C:y²=2px(p>0)的焦点，且与C交于M,N两点，l为C的准线，则【 】
已知抛物线C:y²=8x的焦点为F，点M在C上.若M到直线x=-3距离为5，则|MF|=【 】
已知 A 为抛物线 C : y2 = 2px(p > 0) 上一点, 点 A 到 C 的焦点的距离为 12, 到 y 轴的距离为 9, 则 p=【 】。
设 O 为坐标原点, 直线 x = 2 与抛物线 C : y2 = 2px (p > 0) 交于 D, E 两点, 若 OD ⊥ OE, 则 C 的焦点坐标为【 】
已知向量a ̅=(1,1),b ̅=(1,-1).若(a ̅+λb ̅)⊥(a ̅+μb ̅)，则【 】
已知向量a→,b→满足|a→-b→ |=√3,|a→+b→ |=|2a→-b→|，则|b→ |=________.
已知向量a→,b→满足a→+b→=(2,3),a→-b→=(-2,1)，则|a→ |²-|b→ |²=【 】
已知正方形 ABCD 的边长为 2, 点 P 满足 =1/2(+) ,则|| =______ ; · =______ .
已知向量=(-1,2),=(3,m)，若⊥，则m=________.
在边长为1的等边三角形ABC中，D为线段BC上的动点，DE⊥AB且交AB于点E,DF//AB交AC于点F，则|2+|的值为__________；(+)∙最小值为__________.
设向量a，b的夹角的余弦值为1/3，且|a|=1，|b|=3，则(2a+b)⋅b=_________．
在△ABC中，AC=3,BC=4,∠C=90°．P为△ABC所在平面内的动点，且PC=1，则(PA)⋅(PB)的取值范围是【 】
设点P在单位圆的内接正八边形A1A2…A8的边A1A2上，则(PA1)2+(PA2)2+⋯+(PA8)2的取值范围是_______．