已知 1 < a ⩽ 2, 函数 f(x) = ex − x − a, 其中 e = 2.71828 … 为自然对数的底数.
(I) 证明: 函数 y = f(x) 在 (0, +∞) 上有唯一零点;
(II) 记 x0 为函数 y = f(x) 在 (0, +∞) 上的零点, 证明:
(i) 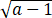 ≤x0≤
≤x0≤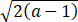 ;
;
(ii) x0 f(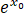 )≥(e-1)(a-1)a .
)≥(e-1)(a-1)a .
已知 1 < a ⩽ 2, 函数 f(x) = ex − x − a, 其中 e = 2.71828 … 为自然对数的底数.
(I) 证明: 函数 y = f(x) 在 (0, +∞) 上有唯一零点;
(II) 记 x0 为函数 y = f(x) 在 (0, +∞) 上的零点, 证明:
(i) 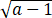 ≤x0≤
≤x0≤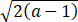 ;
;
(ii) x0 f(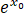 )≥(e-1)(a-1)a .
)≥(e-1)(a-1)a .
(I) 因为 f(0) = 1 − a < 0, f(2) = e2 − 2 − a ⩾ e2 − 4 > 0, 所以 y = f(x) 在 (0, +∞) 上存在零点.因为 f′(x) = ex − 1, 所以当 x > 0 时, f′(x) > 0, 故函数 f(x) 在 (0, +∞) 上单调递增.所以函数 y = f(x) 在 (0, +∞) 上有唯一零点.(II) (i) 令 g(x)=ex-1/2 x2-x-1 (x ⩾ 0), 则 g' (x)=ex-x-1=f(x)+a-1 .由 (i) 知函数 g′(x) 在[0, +∞)上单调递增, 故当 x > 0 时, g′(x) > g′(0) = 0.所以函数 g(x) 在 [0, +∞) 单调递增, 故 g(x) ⩾ g(0) = 0. 由 g()≥0得f()=--a≥0=f(x0) 因为 f(x) 在 [0, +∞) 单调递增, 故 ≥x0.令 h(x) = ex − x2 − x − 1 (0 ⩽ x ⩽ 1), 则 h...
查看完整答案已知方程式2x³+x²+3x+5=0之根为a,b,c,试用变换方程式法求以a(1/b+1/c),b(1/c+1/a),c(1/a+1/b)为根之方程式.
解方程式x5-5x4-5x3+25x2+4x-20=0,已知各根为a,-a,b,-b,c等形式.
鸡蛋每个 80 元,鹅蛋每个 90 元,鸭蛋每个 70 元,用 9700 元买三种蛋共 120个,求各种蛋的个数.
解下列联立方程式x² - 4y² +x + 3y = 2x -y = 1
若x1,x2为方程式2x2-5x+3=0之二根,试求以x1/x2 与x2/x1 为根之方程式.