高中数学-高考试题(北京师范大学 1933年解方程)

计算题（1933年北京师范大学）

试解下列联立方程式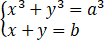

答案解析

暂无答案

讨论

行列式

行列式的值是______.

在n行n列矩阵中，记位于第i行第j列的数为 aij (i,j=1,2,...,n).当n=9时，a11+a22+a33+...a99=________.

定义方程g:[0,π/2]→R为g(θ)=+，其中f(θ)=1/2 +设一元二次函数p(x)的根为方程g(θ)的最大值与最小值，若p(2)=2-√2，则以下说法正确的是【】

非零实数p,q,r分别为调和数列的第10、第100和第1000项，考虑线性方程组列Ⅰ 列Ⅱ(Ⅰ)若q/r=10，则方程组 (P) 有解x=0,y=10/9,z=-1/9(Ⅱ) 若p/r≠100，则方程组 (Q) 有解x=10/9,y=-1/9,z=0(Ⅲ) 若p/q≠10，则方程组 (R) 无穷多解(Ⅳ) 若p/q=10，则方程组 (S) 无解 (T)至少1个解正确的选项为【】

试解下列之联立方程式，求x,y,z之值

东南大学行列式

河北工业大学行列式

已知a∈R，行列式的值与行列式的值相等，则a=________.

南京大学行列式

设x>y>z，证明：1/(yz+zx+xy) <0.

解方程

已知函数 f(x) =.若函数 g(x) = f(x) − |kx2 − 2x| (k ∈ R) 恰有 4 个零点, 则 k 的取值范围是【】.

若x0是方程(1/2 )x=x1/3的解，则x0属于区间【】

解方程log4(3-x)+log0.25(3+x)=log4(1-x)+log0.25(2x+1).

解方程9-x - 2∙31-x = 27.

设f(x)是定义在区间(-∞,+∞)以2为周期的函数，对k∈Z，用Ik表示区间(2k-1,2k+1]，已知当x∈I0时，f(x)=x2.(Ⅰ)求f(x)在Ik上的解析表达式；(Ⅱ)对自然数k,求集合Mk={a|使方程f(x)=ax在Ik 上有两个不相等的实根}.

方程=1/4的解是【】

曲线2y2 + 3x + 3 = 0与曲线x2 + y2 - 4x - 5 = 0 的公共点的个数是【】

方程(1+3-x)/(1+3x)=3的解是______.

已知关于x的实系数二次方程x2+ax+b=0有两个实数根a,β.证明:(I)如果|α|<2,|β|<2,那么2|a|<4+b且|b|<4;(Ⅱ)如果2|a|<4+b且|b|<4,那么|α|<2,β|<2.

某地现有耕地10000公顷，规划10年后粮食单产比现在增加22%,人均粮食占有量比现在提高10%.如果人口年增长率为1%,那么耕地平均每年至多只能减少多少公顷(精确到1公顷)?

函数

如果函数f(x)=x2+bx+c对任意实数t都有f(2+t)=f(2-t)，那么【】

F(x)=(1+)f(x)(x≠0)是偶函数，且f(x)不恒等于零，则f(x)【】

设f(x) = 4x - 2x + 1，则f-1(0) = ________。

定义在(-∞,+∞)上的任意函数f(x)都可以表示成一个奇函数g(x)和一个偶函数h(x)之和,如果 f(x)=lg⁡(10x+1),x∈(-∞,+∞),那么【】

某地为促进淡水鱼养殖业的发展,将价格控制在适当范围内,决定对淡水鱼养殖提供政府补贴.设淡水鱼的市场价格为x元/千克,政府补贴为t元/千克.根据市场调查,当8≤x≤14时,淡水鱼的市场日供应量P千克与市场日需求量Q千克近似地满足关系:P=1000(x+t-8)(x≥9,t≥0),Q=500(8≤x≤14).当P=Q时的市场价格称为市场平衡价格.(1)将市场平衡价格表示为政府补贴的函数,并求出函数的定义域;(2)为使市场平衡价格不高于每千克10元,政府补贴至少为每千克多少元?

设f(x)是(-∞,+∞)上的奇函数, f(x+2)=-f(x)，当0≤x≤1时，f(x)=x，则f(7.5)等于【】

定义在区间(-∞,+∞)上的奇函数f(x)为增函数；偶函数g(x)在区间├ [0,+∞)上的图像与f(x)的图像重合.设a>b>0,给出下列不等式：①f(b)-f(-a)>g(a)-g(-b)；②f(b)-f(-a)<g(a)-g(-b)；③f(a)-f(-b)>g(b)-g(-a)；④f(a)-f(-b)>g(b)-g(-a).其中成立的是【】

函数f(x)=1/x (x≠0)的反函数f-1 (x)=【】

已知映射f:A→B，其中，集合A={-3,-2,-1,1,2,3,4}，集合B中的元素都是A中元素在映射f下的象，且对任意的a∈A，在B中和它对应的元函数是|a|则集合B中元素的个数是【】

若函数y=f(x)的反函数是y=g(x),f(a)=b,ab≠0，则g(b)等于【】