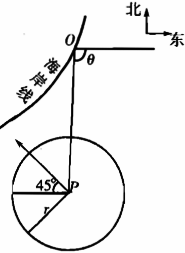
在某海滨城市附近海面有一台风，据监测，当前台风中心位于城市O(如图)的东偏南θ(θ=arccos(√2/10))方向300km的海面P处，并以20km/h的速度向西偏北45°方向移动.台风侵袭的范围为圆形区域，当前半径为60km，并以10km/h的速度不断增大.问几小时后该城市开始受到台风的侵袭?
-
关注优题吧，注册平台账号.
题吧，智能辅助学习中心
问答题（2003年全国旧课程）
答案解析
设在时刻t(h)台风中心为Q，此时台风侵袭的圆形区域半径为10t+60(km).若在时刻t城市O受到台风的侵袭，则OQ≤10t+60，由余弦定理知 OQ2=PQ2+PO2-2∙PQ∙PO∙cos∠OPQ.由于PO=300,PQ=20t，cos∠OPQ=cos(θ-45°)=cosθcos45°+sin...
查看完整答案讨论
已知π/2<β<α<3π/4,cos(α-β)=12/13,sin(α+β)=-3/5,求sin2α的值.
已知θ是第三象限角，且sin4θ + cos4θ = 5/9，那么sin2θ等于【 】
函数y=sin(x - π/6)cosx的最小值是________.
求sin220°+cos250°+sin20°cos50°的值.
当-π/2≤x≤π/2时，函数f(x)=sinx+ cosx 【 】
已知△ABC的三个内角A,B,C满足A+C=2B, 1/cosA +1/cosC =/cosB ,求cos (A-C)/2的值.
(sin7°+cos15°sin8°)/(cos7° - sin15°sin8°)的值为________.
记△ABC的内角A,B,C的对边分别为a,b,c，已知△ABC的面积为√3,D为BC的中点，且AD=1.(1)若∠ADC=π/3，求tanB；(2)若b²+c²=8，求b,c.
△ABC 中, sin2A − sin2B − sin2C = sinBsinC.(1) 求 A;(2) 若 BC = 3, 求 △ABC 周长的最大值.
在 △ABC 中, cosC =2/3, AC = 4, BC = 3, 则 tanB =【 】
已知向量 a, b 满足 |a| = 5, |b| = 6, a · b = −6, 则 cos⟨a, a + b⟩ =【 】
在 △ABC 中, cosC = 2/3 , AC = 4, BC = 3, 则 cosB =【 】
圆之直径 AB 上任意取 P 点，又 CD 与直径平行，求证 AP² + BP²=CP² + DP².
A,B,C 为三定点，求作一圆过 A,B，使从 C 到此圆的切线等于定长.
已知PA,PB,PC为过圆周上点P三弦，PT为圆之切线，设有一直线与PT平行，交PA,PB,PC于A',B',C'三点.求证：PA∙PA'=PB∙PB'=PC∙PC'.
如图，AB是⊙O的直径，CB是⊙O的切线，切点为B，OC平行于弦AD.求证：DC是⊙O的切线.
已知：如图，MN为圆的直径，P、C为圆上两点，连PM、PN，过C作MN的垂线与MN、MP和NP的延长线依次相交于A、B、D，求证：AC2=AB·AD.
有一个圆内接三角形ABC，∠A的平分线交BC于D，交外接圆于E，求证：AD·AE=AC·AB.