关注优题吧，注册平台账号.
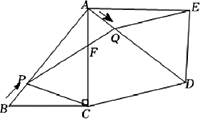
如图，在Rt△ABC中，∠ACB=90°,AB=5cm,BC=3cm，将△ABC绕点A按逆时针方向旋转90°得到△ADE，连接CD.点P从点B出发，沿BA方向匀速运动,速度为1cm/s，同时，点Q从点A出发，沿AD方向匀速运动，速度为1m/s. PQ交AC于点F，连接CP,EQ，设运动时间为t(s)(0<t<5).
解答下列问题：
(1)当EQ⊥AD时，求t的值;
(2)设四边形PCDQ的面积为S(cm^2)，求S与t之间的函数关系式;
(3)是否存在某一时刻t，使PQ//CD?若存在，求出t的值；若不存在，请说明理由.
(1)如图，在Rt△ABC中，AC==4，∵将△ABC绕点A按逆时针方向旋转90°得到△ADE，∴AD=AB=5,DE=BC=3,AE=AC=4,∠AED=∠ACB=90°,∵EQ⊥AD∴∠AQE=∠AED=90°,∠EAQ=∠DAE,∴△AQE~△AED∴AQ/AE=AE/AD,即AQ/4=4/5,∴AQ=16/5,∴t=AQ/1=16/5.(2)过P作PN⊥BC于N，过C作CM⊥AD于M,∵将△ABC绕点A按逆时针方向旋转90°得到△ADE，∴∠BAD=90°，即∠BAC+∠CAM=90°,∵∠B+∠BAC=90°,∴∠B=∠CAM,∴△ABC~△CAM,∴AC/CM=AB/AC，即4/CM=5/4，∴CM=16/5,∴S△ACD=1/2 AD∙CM=1/2×5×16/5=8,∴SABCD=S△...
查看完整答案泰勒斯是古希腊时期的思想家，科学家，哲学家，他最早提出了命题的证明．泰勒斯曾通过测量同一时刻标杆的影长，标杆的高度。金字塔的影长，推算出金字塔的高度。这种测量原理，就是我们所学的【 】
已知ΔABC的周长为16，点D，E，F分别为ΔABC三条边的中点，则ΔDEF的周长为【 】
如图，BC//DE,且BC<DE,AD=BC=4,AB+DE=10，则AE/AC的值为__________.
如图，在ΔABC中，M，N分别是AB和AC的中点，连接MN，点E是CN的中点，连接ME并延长，交BC的延长线于点D，若BC=4，则CD的长为_________.
如图，每个小正方形边长均为1，则图中的三角形(阴影部分)与下图中△ABC相似的是【 】
如图，△ABC与△DEF均为等边三角形，O为BC、EF的中点，则AD:BE的值为【 】
在Rt△ABC中，∠C=90°,AD平分∠CAB,BE平分∠ABC,AD,BE相交于点F，且AF=4,EF=√2，则AC=________.
如图，在方格纸中，将Rt△AOB绕点B按顺时针方向旋转90°后得到Rt△A′O′B，则下列四个图形中正确的是【 】
如图，在边长为6的正方形ABCD内作∠EAF=45°，AE交BC于点E，AF交CD于点F，连接EF，将ΔADF绕点A顺时针旋转90°得到ΔABG.若DF=3，则BE的长为__________.
如图的四个三角形中，不能由△ABC经过旋转或平移得到的是【 】
如图，在△ABC中，AB=AC，若M是BC边上任意一点，将△ABM绕A逆时针旋转得到△ACN，点M的对应点为点N，连接MN，则下列结论一定正确的是【 】
如图，将ΔABC先向右平移3个单位，再绕原点O旋转180°得到ΔA'B'C'，则点A的对应点A'的坐标是【 】
如图，在正方形ABCD中，AB=3，点E，F分别在边AB，CD上，∠EFD=60°.若将四边形EBCF沿EF折叠，点B恰好落在AD边上，则BE的长度为【 】