初中数学-中考试题(天津市 2022年旋转)

问答题（2022年天津市）

将一个矩形纸片OABC放置在平面直角坐标系中，点O(0,0),A(3,0),C(0,6)，点P在边OC上(点P不与点O,C重合)，折叠该纸片，使折痕所在的直线经过点P，并与x轴的正半轴相交于点Q,且∠OPQ=30°，点O的对应点O'落在第一象限.设OQ=t.

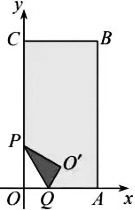
(I)如图①，当t=1时，求∠O'QA的大小和点O'的坐标:

(Ⅱ)如图②，若折叠后重合部分为四边形，O' Q,O'P分别与边AB相交于点E,F，试用含有t的式子表示O'E的长，并直接写出t的取值范围:

(Ⅲ)若折叠后重合部分的面积为3√3，则t的值可以是__________(请直接写出两个不同的值即可).

答案解析

(I)在Rt△POQ中，由∠OPQ=30°可知∠OQP=90°-30°=60°.根据折叠，知△POQ≅△PO'Q，∴O' Q=OQ,∠O' QP=∠OQP=60°,∴∠O' QA=180°-∠OQP-∠O' QP=60°.如图，过点O'作O'H⊥OA，垂足为H，则∠O' HQ=90°.∴在Rt△O'HQ中，∠QO' H=90°-∠O' QA=30°.由t=1得OQ=1,O' Q=1.由QH=1/2 O' Q=1/2,O' H2+QH2=O' Q2得OH=OQ+QH=3/2,O' H==√3/2.∴点O'的坐标为(3/2,√3/2). (Ⅱ)∵点A(3,0),∴OA=3,又OQ=t，∴QA=OA-OQ=3-t.由(I)知O' Q=t,∠O' QA=6...

查看完整答案

讨论

旋转

如图,四边形ABCO是平行四边形，AO=2,AB=6，点C在x轴的负半轴上，将ABCO绕点A逆时针旋转得到ADEF,AD经过点O，点F恰好落在x轴的正半轴上，若点D在反比例函数y=k/x的图像上，则k的值为________.

如图，在方格纸中，将Rt△AOB绕点B按顺时针方向旋转90°后得到Rt△A′O′B，则下列四个图形中正确的是【】

如图，在由边长为1个单位长度的小正方形组成的网格中，△ABC的顶点均为格点（网格线的交点）.（1）将△ABC 向上平移6个单位，再向右平移2个单位，得到△A1B1C1，请画出△A1B1C1﹔（2）以边AC的中点O为旋转中心，将△ABC 按逆时针方向旋转180°，得到△A2B2C2，请画出△A2B2C2．

如图，在边长为6的正方形ABCD内作∠EAF=45°，AE交BC于点E，AF交CD于点F，连接EF，将ΔADF绕点A顺时针旋转90°得到ΔABG.若DF=3，则BE的长为__________.

如图的四个三角形中，不能由△ABC经过旋转或平移得到的是【】

在△ABC中，∠ACB＝90°，CD是中线，AC＝BC，一个以点D为顶点的45°角绕点D旋转，使角的两边分别与AC、BC的延长线相交，交点分别为点E、F，DF与AC交于点M，DE与BC交于点N．（1）如图1，若CE＝CF，求证：DE＝DF；（2）如图2，在∠EDF绕点D旋转的过程中，试证明CD2＝CE•CF恒成立；（3）若CD＝2，CF＝，求DN的长．

如图，方格纸中的每个小方格都是边长为1个单位的正方形，Rt△ABC的顶点均在某个点上，在建立平面直角坐标系后，点A的坐标为(-6，1)，点B的坐标为(-3，1)点C的坐标为(-3，3).(1)将Rt△ABC沿x轴正方向平移5个单位得到Rt△A1B1C1，试在图上画出的图形Rt△A1B1C1，并写出点A1的坐标；(2)将原来的R△ABC绕点B顺时针旋转90°得到Rt△A2B2C2，试在图上画出Rt△A2B2C2的图形.

如图，在△ABC中，AB=AC，若M是BC边上任意一点，将△ABM绕A逆时针旋转得到△ACN，点M的对应点为点N，连接MN，则下列结论一定正确的是【】

如图，在正方形ABCD中，AB=3，点E，F分别在边AB，CD上，∠EFD=60°.若将四边形EBCF沿EF折叠，点B恰好落在AD边上，则BE的长度为【】

如图，在Rt△ABC中，∠ACB=90°,AB=5cm,BC=3cm，将△ABC绕点A按逆时针方向旋转90°得到△ADE，连接CD.点P从点B出发，沿BA方向匀速运动,速度为1cm/s，同时，点Q从点A出发，沿AD方向匀速运动，速度为1m/s. PQ交AC于点F，连接CP,EQ，设运动时间为t(s)(0<t<5).解答下列问题：(1)当EQ⊥AD时，求t的值;(2)设四边形PCDQ的面积为S(cm^2)，求S与t之间的函数关系式;(3)是否存在某一时刻t，使PQ//CD?若存在，求出t的值；若不存在，请说明理由.

直角三角形

如图，ΔABC中，点E在边AC上，EB=EA，∠A=2∠CBE，CD垂直于BE的延长线于点D，BD=8，AC=11，则边BC的长为_______．

脱贫攻坚工作让老百姓过上了幸福的生活．如图①是政府给贫困户新建的房屋，如图②是房屋的侧面示意图，它是一个轴对称图形，对称轴是房屋的高AB所在的直线．为了测量房屋的高度，在地面上C点测得屋顶A的仰角为35°，此时地面上C点、屋檐上E点、屋顶上A点三点恰好共线，继续向房屋方向走8m到达点D时，又测得屋檐E点的仰角为60°，房屋的顶层横梁EF=12m，EF//CB，AB交EF于点G（点C，D，B在同一水平线上）。（参考数据：sin⁡3 5°≈0.6，cos⁡3 5°≈0.8，tan⁡3 5°≈0.7，≈1.7）（1）求屋顶到横梁的距离AG；（2）求房屋的高AB（结果精确到1m）．

如图，在△ABC中，∠C=90°,tan⁡A=/3,∠ABC的平分线BD交AC于点D.CD=.求AB的长？

如图，在RtΔABC中，∠ACB=90°，AC=BC=2，CD⊥AB于点D.点P从点A出发，沿A→D→C的路径运动，运动到点C停止，过点P作PE⊥AC于点E，作PF⊥BC于点F.设点P运动的路程为x，四边形CEPF的面积为y，则能反映y与x之间函数关系的图象是【】

一副直角三角板如图放置，点C在FD的延长线上，AB//CF，∠F＝∠ACB＝90°，则∠DBC的度数为【】

如图，已知Rt△ABC中，斜边BC上的高AD=4，cosB=4/5，则AC=______.

已知两个全等的直角三角形纸片ABC、DEF，如图(1)放置，点B、D重合，点F在BC上，AB与EF交于点G，∠C=∠EFB=90°，∠E=∠ABC=30°，AB=DE=4. (1)求证：△EGB是等腰三角形；(2)若纸片DEF不动，问△ABC绕点F逆时针旋转最小______度时，四边形ACDE成为以ED为底的梯形(如图(2)).求此梯形的高.

如图， RT△ABC中∠C=90°，以斜边AB为边向外作正方形ABDE，且正方形对角线交于点O，连接OC，已知AC=5,OC=6，则另一直角边BC的长为________.

如图，为了测量河对岸两点AB之间的距离，在河岸这边取点CD测得CD=80m，∠ACD=90°，∠BCD=45°，∠ADC=19°17'，∠BDC=56°19'，设A，B，C，D在同一平面内，求A，B两点之间的距离.(参考数据：tan19°17'≈0.35，tan56°19'≈1.50.)

在△ABC中，∠ABC=90°，若AC=100,sinA=3/5，则AB的长是【】

平面直角坐标系

如图，平面直角坐标系中，点B在第一象限，点A在x轴的正半轴上，∠AOB＝∠B＝30°，OA＝2．将△AOB绕点O逆时针旋转90°，点B的对应点B'的坐标是【】

如图，△OAB的顶点O(0,0)，顶点A,B分别在第一、四象限，且AB⊥x轴，若AB=6,OA=OB=5，则点A的坐标是【】

如图，已知点A(5,2),B(5，4),C(8，1)，直线l⊥x轴，垂足为点M(m，0),其中m<5/2，若△A'B'C'与△ABC关于直线l对称，且△A'B'C'有两个顶点在函数y=k/x(k≠0)的图像上，则k的值为__________.

已知点P(a-1,a+2)在平面直角坐标系的第二象限内,则a的取值范围在数轴上可表示为【】

如图(左)所示,以点M(-1,0)为圆心的圆与y轴,x轴分别交于点A,B,C,D,直线y=-/3 x-5/3与⊙M相切于点H,交x轴于点E,交y轴于点F. (1)请直接写出OE,⊙M的半径r，CH的长;(2)如图(中)所示,弦HQ交x轴于点P,且DP:PH=3:2,求cos∠QHC的值;(3)如图(右)所示,点K为线段EC上一动点(不与E,C重合),连接BK交⊙M于点T,弦AT交ⅹ轴于点N.是否存在一个常数a,始终满足MN•MK=a,如果存在,请求出a的值;如果不存在,请说明理由.

已知点P(a+1,2a-3)关于x轴的对称点在第一象限，则a的取值范围是【】

抛物线y=x2-1交x轴于A,B两点(A在B的左边),(1) ▱ACDE的顶点C在y轴的正半轴上，顶点E在y轴右侧的抛物线上.①如图(1)，若点C的坐标是(0,3)，点E的横坐标是5，直接写出点A,D的坐标;②如图(2)，若点D在抛物线上，且▱ACDE的面积是12，求点E的坐标.(2)如图(3)，F是原点O关于抛物线顶点的对称点，不平行y轴的直线l分别交线段AF,BF(不含端点)于G,H两点.若直线l与抛物线只有一个公共点，求证：FG+FH的值是定值.

在平面直角坐标系xOy中，点M(-4，2)关于x轴对称的点的坐标是【】

如图所示，将正方形OEFG放在平面直角坐标系中，O是坐标原点，点E的坐标为(2,3)，则点F的坐标为_________.

如图，在平面直角坐标系中，ΔOAB的顶点A，B的坐标分别为(3,)，(4,0).把ΔOAB沿x轴向右平移得到ΔCDE，如果点D的坐标为(6,)，则点E的坐标为_________.