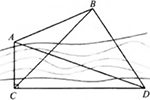
如图，为了测量河对岸两点AB之间的距离，在河岸这边取点CD测得CD=80m，∠ACD=90°，∠BCD=45°，∠ADC=19°17'，∠BDC=56°19'，设A，B，C，D在同一平面内，求A，B两点之间的距离.(参考数据：tan19°17'≈0.35，tan56°19'≈1.50.)
-
关注优题吧，注册平台账号.
题吧，智能辅助学习中心
问答题（2021年江苏省南京市）
答案解析
如图，作BE⊥CD于E,作BF⊥CA交CA延长线于F. ∵∠FCD=90°∴四边形CEBF是矩形，∵BE⊥CD,∠BCD=45°,∴∠BCE=∠CBE=45°,∴CE=BE,∴矩形CEBF是正方形.设CE=BE=xm，在Rt△BDE中，DE=BE/(tan∠BDE)=x/(tan56°19')≈2/3 xm.∵CD...
查看完整答案讨论
如图，在△ABC中，AD平分∠BAC，DE⊥AB，若AC=2,DE=1，则S△ACD=________.
已知点O是边长为6的等边△ABC的中心，点P在△ABC外，△ABC，△PAB，△PBC，△PCA 的面积分别记为S0,S1,S2,S3．若S1+S2+S3=S0，则线段OP长的最小值是【 】
如图，已知△ABC，AB<BC，用尺规作图的方法在BC 上取一点P，使得PA+PC=BC，则下列选项正确的是【 】
在Rt△ABC中，∠C=90°,AD平分∠CAB,BE平分∠ABC,AD,BE相交于点F，且AF=4,EF=√2，则AC=________.
泰勒斯是古希腊时期的思想家，科学家，哲学家，他最早提出了命题的证明．泰勒斯曾通过测量同一时刻标杆的影长，标杆的高度。金字塔的影长，推算出金字塔的高度。这种测量原理，就是我们所学的【 】
如图，AB//CD，∠B=∠D，直线EF与AD，BC的延长线分别交于点E，F.求证:∠DEF=∠F.
如图，在平行四边形ABCD中，将△AB' C沿着AC所在的直线翻折得到△AB' C,B'C交AD于点E，连接B'D.若∠B=60°,∠ACB=45°,AC=.则B'D的长是【 】
如图，在Rt△ABC中，∠C=90°.AF=EF.若∠CFE=72°.则∠B=______°.
如图，四边形ABCD为菱形，∠ABC=70°，延长BC到E，在∠DCE内作射线CM，使得∠ECM=15°，过点D作DF⊥CM，垂足为F若DF=，则对角线BD的长为________(结果保留根号)
如图，已知菱形ABCD的边长为2，∠DAB=60°，E为AB的中点，F为CE的中点，AF与DE相交于点G，则GF的长等于________.
如图，扇形纸片AOB的半径为3，沿AB折叠扇形纸片，点O恰好落在(AB) ̂上的C处，图中阴影部分的面积为【 】