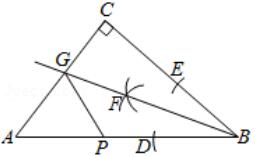
如图,RtΔABC中,∠C=90°,利用尺规在BC,BA上分别截取BE,BD,使BE=BD;分别以D,E为圆心、以大于1/2 DE的长为半径作弧,两弧在∠CBA内交于点F;作射线BF交AC于点G.若CG=1,P为AB上一动点,则GP的最小值为【 】
A、无法确定
B、1/2
C、1
D、2
如图,RtΔABC中,∠C=90°,利用尺规在BC,BA上分别截取BE,BD,使BE=BD;分别以D,E为圆心、以大于1/2 DE的长为半径作弧,两弧在∠CBA内交于点F;作射线BF交AC于点G.若CG=1,P为AB上一动点,则GP的最小值为【 】

A、无法确定
B、1/2
C、1
D、2
C
如图,在Rt△ABC中,∠A=90°,作BC的垂直平分线交AC于点D,延长AC至点E,使CE=AB. (1)若AE=1,求△ABD的周长;(2)若AD=1/3 BD,求tan∠ABC的值.
如图,在Rt△ABC中,∠C=90°,AC=6,BC=8,将△ABC绕点A逆时针旋转得到△AB'C',使点C'落在AB边上,连结BB',则sin∠BB'C'的值为【 】
如图,在Rt△ABC中,∠C=90°,∠A=30°,线段AB的垂直一部分线分别交AC、AB于点D、E,连接BD.若CD=1,则AD的长为________.
如图,数字代表所在正方形的面积,则A所代表的正方形的面积为________.
用直尺、圆规作图,不写作法,但要保留作图痕迹.已知:Rt△ABC,∠B=90°.求作:点P使点P在△ABC内部,且PB=PC,∠PBC=45°.
如图,点O在直线AB上OC⊥OD.若∠AOC=120°,则∠BOD的大小为【 】.
如图,正方形纸板的一条对角线垂直于地面,纸板上方的灯(看作一个点)与这条对角线所确定的平面垂直于纸板,在灯光照射下,正方形纸板在地面上形成的影子的形状可以是【 】
为庆祝中国共产党建党100周年,某校用红色灯带制作了一个如图所示的正五角星(A,B,C,DE是正五边形的五个顶点),则图中∠A的度数是度______°.
如图是一个正方体的展开图,把展开图折叠成小正方体后,和“建”字所在面相对的面上的字是【 】
如图,在点F处,看建筑物顶端D的仰角为32°,向前走了15米到达点E即EF=15米,在点E处看点D的仰角为64°,则CD的长用三角函数表示为【 】