如图,在Rt△ABC中,∠C=90°,∠A=30°,线段AB的垂直一部分线分别交AC、AB于点D、E,连接BD.若CD=1,则AD的长为________.
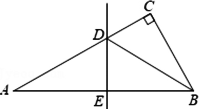
如图,在Rt△ABC中,∠C=90°,∠A=30°,线段AB的垂直一部分线分别交AC、AB于点D、E,连接BD.若CD=1,则AD的长为________.

2
【解析】
∵DE垂直平分AB,∴AD=BD,∴∠A=∠ABD,
∵∠A=30°,∴∠ABD=30°,∴∠BDC=∠A+∠ABD=30°+30°=60°,
∵∠C=90°,∴∠CBD=30°,
∵CD=1.∴BD=2CD=2,∴AD=2.
在△ABC中,∠ABC=90°,若AC=100,sinA=3/5,则AB的长是【 】
小明去爬山,在山脚看山顶角度为30°,小明在坡比为5:12的山坡上走1300米,此时小明看山顶的角度为 60°,求山高【 】
如图,在RtΔABC中,∠ACB=90°,AC=3,BC=4,CD⊥AB,垂足为D,E为BC的中点,AE与CD交于点F,则DF的长为_______.
如图所示,某校数学兴趣小组利用标杆BE测量建筑物的高度,已知标杆BE高1.5m,测得AB=1.2m,BC=12.8m,则建筑物CD的高是【 】
如图所示,∠AOB是放置在正方形网格中的一个角,则sin∠AOB的值是________.
如图,ΔABC中,点E在边AC上,EB=EA,∠A=2∠CBE,CD垂直于BE的延长线于点D,BD=8,AC=11,则边BC的长为_______.
如图,在△ABC中,∠C=90°,tanA=/3,∠ABC的平分线BD交AC于点D.CD=.求AB的长?
已知△ABC的三个顶点都是同一个正方形的顶点,∠ABC的平分线与线段AC交于点D.若△ABC的一条边长为6,则点D到直线AB的距离为________.(结果要化简,不能含三角函数)
如图,已知点O是△ABC的外心,∠A=40°,连结BO、CO则∠BOC的度数是【 】
如图,在△ABC中,点D、E分别是BC、AC的中点,AD与BE相交于点F,若BF=6,则BE的长是________.
如图,在△ABC中,AD平分∠BAC,DE⊥AB,若AC=2,DE=1,则S△ACD=________.
已知点O是边长为6的等边△ABC的中心,点P在△ABC外,△ABC,△PAB,△PBC,△PCA 的面积分别记为S0,S1,S2,S3.若S1+S2+S3=S0,则线段OP长的最小值是【 】
泰勒斯是古希腊时期的思想家,科学家,哲学家,他最早提出了命题的证明.泰勒斯曾通过测量同一时刻标杆的影长,标杆的高度。金字塔的影长,推算出金字塔的高度。这种测量原理,就是我们所学的【 】