关注优题吧，注册平台账号.
在正方形ABCD中，等腰直角△AEF, ∠AFE=90°，连接CE，H为CE的中点，连接BH、BF、HF，发现BF/BH和∠HBF为定值.
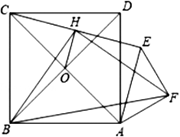
(1)①BF/BH=________;
②∠HBF=________;
③小明为了证明①②，连接AC交BD于O,连接OH，证明了OH/AF和BA/BO的关系，请你按他的思路证明①②.
(2)小明又用三个相似三角形（两个大三角形全等）摆出下图，BD/AD=EA/FA=k,∠BDA=∠EAF=θ(0°<θ<90°).
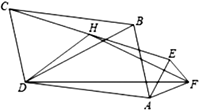
①FD/HD=________(用k的代数式表示)
②FH/HD=________(用k,θ的代数式表示)
(1)①√2;②45°③由正方形的性质得：AB/BO=√2.O为AC的中点,又∵H为CE的中点，∴OH//AE,OH=1/2 AE,∵△AEF是等腰直角三角形，∴AE=√2 AF,∴AF/OH=√2=AB/BO,∵OH//AE,∴∠COH=∠CAE,∴∠BOH=∠BAF,∴△BOH∼△BAF,∴BF/BH=√2,∠HBF=∠HBO+∠OBF=∠FBA+∠OBF=45°.(2)①如图，连接AC交BD于O...
查看完整答案泰勒斯是古希腊时期的思想家，科学家，哲学家，他最早提出了命题的证明．泰勒斯曾通过测量同一时刻标杆的影长，标杆的高度。金字塔的影长，推算出金字塔的高度。这种测量原理，就是我们所学的【 】
已知ΔABC的周长为16，点D，E，F分别为ΔABC三条边的中点，则ΔDEF的周长为【 】
如图，BC//DE,且BC<DE,AD=BC=4,AB+DE=10，则AE/AC的值为__________.
如图，每个小正方形边长均为1，则图中的三角形(阴影部分)与下图中△ABC相似的是【 】
如图，△ABC与△DEF均为等边三角形，O为BC、EF的中点，则AD:BE的值为【 】
如图，在ΔABC中，M，N分别是AB和AC的中点，连接MN，点E是CN的中点，连接ME并延长，交BC的延长线于点D，若BC=4，则CD的长为_________.
在Rt△ABC中，∠C=90°,AD平分∠CAB,BE平分∠ABC,AD,BE相交于点F，且AF=4,EF=√2，则AC=________.
观察下列算式,用你所发现的规律得出22015的末位数字是【 】21=2,22=4,23=8,24=16,25=32,26=64,27=128,28=256,…
如图是两个可以自由转动的转盘，转盘各被等分成三个扇形，并分别标上1，2，3和6，7，8这6个数字.如果同时转动两个转盘各一次(指针落在等分线上重转)，转盘停止后，则指针指向的数字和为偶数的概率是【 】
如图，在△ABC中，AB的垂直平分线交AB于点D，交BC于点E，连接AE．若BC＝6，AC＝5，则△ACE的周长为【 】
如图，已知点O是△ABC的外心，∠A=40°，连结BO、CO则∠BOC的度数是【 】
如图，在△ABC中，点D、E分别是BC、AC的中点，AD与BE相交于点F，若BF=6，则BE的长是________.
如图，在Rt△ABC中，∠A=90°，作BC的垂直平分线交AC于点D，延长AC至点E，使CE=AB. (1)若AE=1，求△ABD的周长;(2)若AD=1/3 BD，求tan∠ABC的值.
如图，边长为1的正方形ABCD中，点E为AD的中点，连接BE，将ABE沿BE折叠得到△FBE，BF交AC于点G，求CG的长.
如图，已知∠BAC=60°，AD是角平分线且AD=10，作AD的垂直平分线交AC于点F，作DE⊥AC，则△DEF的周长为____________.