初中数学-中考试题(浙江省湖州市 2021年三角形)

单项选择（2021年浙江省湖州市）

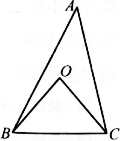
如图，已知点O是△ABC的外心，∠A=40°，连结BO、CO则∠BOC的度数是【】

A、60°

B、70°

C、80°

D、90°

答案解析

C

讨论

初中数学

将如图所示的长方体牛奶包装盒沿某些棱剪开且使六个面连在一起然后铺平则得到的图形可能是【】

下列事件中，属于不可能事件的是【】

不等式3x-1>5的解集是【】

化简√8的正确结果是【】

实数-2的绝对值是【】

在几何体表面上，蚂蚁怎样爬行路径最短?(1)如图①，圆锥的母线长为12cm，B为母线OC的中点，点A在底面圆周上，AC的长为4πcm.在图②所示的圆锥的侧面展开图中画出蚂蚁从点A爬行到点B的最短路径，并标出它的长(结果保留根号).① ②(2)图③中的几何体由底面半径相同的圆锥和圆柱组成.O是圆锥的顶点，点A在圆柱的底面圆周上.设圆锥的母线长为l，圆柱的高为h.③ ④①蚂蚁从点A爬行到点O的最短路径的长为________(用含l,h的代数式表示).②设AD的长为a,点B在母线OC上，OB=b.圆柱的侧面展开图如图④所示，在图中画出蚂蚁从点A爬行到点B的最短路径的示意图，并写出求最短路径的长的思路.

已知二次函数y=ax2+bx+c的图像经过(-2,1),(2-3)两点.(1)求b的值.(2)当c>-1时，该函数的图像的顶点的纵坐标的最小值是__________.(3)设(m,0)是该函数的图像与x轴的一个公共点，当-1<m<3时，结合函数的图像，直接写出a的取值范围.

如图，已知P是⊙O外一点.用两种不同的方法过点P作⊙O的一条切线.要求:(1)用直尺和圆规作图;(2)保留作图的痕迹，写出必要的文字说明.

甲、乙两人沿同一直道从A地去B地,甲比乙早1min出发,乙的速度是甲的2倍.在整个行程中，甲离A地的距离y1(单位:m)与时间x(单位:min)之间的函数关系如图所示.(1)在图中画出乙离A地的距离y2(单位:m)与时间x之间的函数图;(2)若甲比乙晚5min到达B地，求甲整个行程所用的时间.

如图，为了测量河对岸两点AB之间的距离，在河岸这边取点CD测得CD=80m，∠ACD=90°，∠BCD=45°，∠ADC=19°17'，∠BDC=56°19'，设A，B，C，D在同一平面内，求A，B两点之间的距离.(参考数据：tan19°17'≈0.35，tan56°19'≈1.50.)

三角形

如图，四边形ABCD是矩形，延长DA到点E，使AE=DA，连接EB，点F1是CD的中点，连接EF1，BF1，得到ΔEF1B；点F2是CF_1的中点，连接EF2，BF2，得到ΔEF2 B；点F3是CF2的中点，连接EF3，BF3，得到ΔEF3 B；…；按照此规律继续进行下去，若矩形ABCD的面积等于2，则ΔEFn B的面积为_________.（用含正整数n的式子表示）

如图，在△ABC中，AB的垂直平分线交AB于点D，交BC于点E，连接AE．若BC＝6，AC＝5，则△ACE的周长为【】

如图，△ABC的内心在y轴上，点C的坐标为(2，0)，点B的坐标是(0，2)，直线AC的解析式为y=1/2 x-1，则tanA的值是______.

问题提出如图(1)，在△ABC和△DEC中，∠ACB=∠DCE=90°，BC=AC，EC=DC，点E在△ABC内部，直线AD与BE交于点F.线段AF，BF，CF之间存在怎样的数量关系?问题探究(1)先将问题特殊化.如图(2)，当点D，F重合时，直接写出一个等式，表示AF，BF，CF之间的数量关系;(2)再探究一般情形.如图(1)，当点D，F不重合时，证明(1)中的结论仍然成立.问题拓展如图(3)，在△ABC和△DEC中，∠ACB=∠DCE=90°，BC=kAC，EC=kDC(k是常数)，点E在△ABC内部，直线AD与BE交于点F.直接写出一个等式，表示线段AF，BF，CF之间的数量关系.

如图，在平面直角坐标系中，△AOB的边AO、AB的中点C、D的横坐标分别是1、4，则点B的横坐标是______.

如图，在四边形ABCD中，AB=BC=BD.设∠ABC=α，则∠ADC______(用含α的代数式表示).

【图形定义】有一条高线相等的两个三角形称为等高三角形，例如：如图①，在∆ABC和∆A'B'C'中，AD，A'D'分别是BC和B'C'边上的高线，且AD=A'D'、则∆ABC和∆A'B'C'是等高三角形。【性质探究】如图①，用S∆ABC和S∆A'B'C'分别表示∆ABC和∆A'B'C'的面积，则S∆ABC=1/2 BC∙AD,S∆A' B' C'=1/2 B'C'∙A'D',∵AD=A'D'∴S∆ABC:S∆A'B'C'=BC:B'C'.【性质应用】(1)如图②，D是△ABC的边BC上的一点.若BD=3，DC=4，则S∆ABD:S∆ADC=________;(2)如图③，在ΔABC中，D，E分别是BC和AB边上的点.若BE:AB=1:2,CD:BC=1:3,S∆ABC=1,则S∆BEC=______, S∆DEC=________.(3)如图③，在ΔABC中，D，E分别是BC和AB边上的点. 若BE:AB=1:m,CD:BC=1:n,S∆ABC=a,则S∆DEC=________.

如图，将△ABC折叠，使AC边落在△AB边上，展开后得到折痕l，则l是ABC的【】

如图，将三角形纸片剪掉一角得四边形，设△ABC与四边形BCDE的外角和的度数分别为a，β，则正确的是【】

题目:“如图，∠B=45°，BC=2，在射线BM上取一点A，设AC=d，若对于d的一个数值，只能作出唯一一个△ABC，求d的取值范围.”对于其答案，甲答：d≥2；乙答：d=1.6；丙答：d=√2，则正确的是【】

几何图形

如图，在平面直角坐标系中，点P的坐标为(-4，0)，⊙P的半径为2，将⊙P沿x轴向右平移4个单位长度得⊙P1.(1)画出⊙P1，并直接判断⊙P与⊙P1的位置关系；(2)设⊙P1与x轴正半轴，y轴正半轴的交点分别为A、B.求劣弧AB与弦AB围成的图形的面积(结果保留π).

下列图形中,是中心对称图形,但不是轴对称图形的是【】

在平面直角坐标系xOy中，已知点M(a,b),N.对于点P给出如下定义：将点P向右(a≥0)或向左(a<0)平移|a|个单位长度，再向上(b≥0)或向下(b<0)平移|b|个单位长度，得到点P'，点P'关于点N的对称点为Q，称点Q为点P的“对应点”.(1)如图，点M(1,1),点N在线段OM的延长线上，若点P(-2,0),点Q为点P的“对应点”. ①在图中画出点Q;②连接PQ.交线段ON于点T.求证：NT=1/2 OM.(2) ⨀O的半径为1，M是⨀O上一点，点N在线段OM上，且ON=t(1/2<t<1)，若P为⨀O外一点，点Q为点P的“对应点”,连接PQ.当点M在⨀O上运动时直接写出PQ长的最大值与最小值的差(用含t的式子表示).

一个由长方体截去一部分后得到的几何体如图水平放置，其俯视图是【】

下列图形中是轴对称图形但不是中心对称图形的是【】

由几个大小相同的正方形组成的几何图形如图，则它的俯视图是【】

下列图形既是中心对称又是轴对称图形的是【】

下列主视图正确的是【】

下列图形中，是轴对称图形的是【】

把下列图标折成一个正方体的盒子，折好后与“中”相对的字是【】