中考2015年广东省广州市( )
已知O为坐标原点,抛物线y=ax²+bx+c(a≠0)与x轴相交于点A(x1,0),B(x2,0),与y轴交于点C,且OC两点间的距离为3,x1 x2<0,|x1 |+|x2 |=4,点A,C在直线y2=-3x+t上.
(1)求点C的坐标;
(2)当y随着x的增大而增大时,求自变量x的取值范围;
(3)当抛物线y向左平移n(n>0)个单位,记平移后y随着x的增大而增大的部分为P,直线y2向下平移n个单位,当平移后的直线与P有公共点时,求2n²-5n的最小值.
解答过程见word版
中考2015年广东省广州市( )
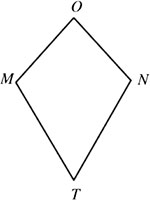
如图,四边形OMTN中,OM=ON,TM=TN,我们把这种两组邻边分别相等的四边形叫做筝形.
(1)试探究筝形对角线之间的位置关系,并证明你的结论;
(2)在筝形ABCD中,已知AB=AD=5,BC=CD,BC>AB,BD、AC为对角线,BD=8.
①是否存在一个圆使得 A、B、C、D四个点都在这个圆上?若存在,求出圆的半径;若不存在,请说明理由;
②)过点B作BF⊥CD,垂足为F,BF交AC于点E,连接DE,当四边形 ABED为菱形时,求点F到 AB 的距离.
解答过程见word版
中考2015年广东省广州市( )
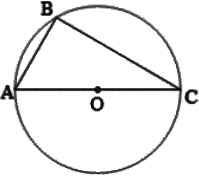
如图,AC是⊙O的直径,点B在⊙O上,∠ACB=30°.
(1)利用尺规作∠ABC的平分线BD,交AC于点E,交⊙O于点D,连接CD(保留作图痕迹不写作法);
(2)在(1)所作的图形中,求△ABE与△CDE的面积之比.
解答过程见word版
中考2015年广东省广州市( )
4件同型号的产品中,有1件不合格品和3件合格品.
(1)从这4件产品中随机抽取1件进行检测,求抽到的是不合格品的概率;
(2)从这4件产品中随机抽取2件进行检测,求抽到的都是合格品的概率;
(3)在这4件产品中加入x件合格品后,进行如下试验:随机抽取1件进行检测,然后放回,多次重复这个试验,通过大量重复试验后发现:抽到合格品的频率稳定在0.95,则可以推算出x的值大约是多少?
解答过程见word版
中考2015年广东省广州市( )
某地区2013年投入教育经费2500万元,2015年投入教育经费3025万元.
(1)求2013年到2015年该地区投入教育经费的年平均增长率;
(2)根据(1)所得的年平均增长率,预计2016年该地区将投入教育经费多少万元.
(1)设2013年至2015年该地区投入教育经费的年平均增长率为x,
由题意得:2500(1+x)²=3025.
解得:x1=0.1,x2=-2.1(舍去)
所以,增长率为10%.
答:2013年至2015年该地区投入教育经费的年平均增长率为10%.
(2)由题意得:3025×(1+10%)=3327.5(万元)
答:2016年该地区将投入教育经费3327.5万元.

