中考2015年广东省广州市( )
已知O为坐标原点,抛物线y=ax²+bx+c(a≠0)与x轴相交于点A(x1,0),B(x2,0),与y轴交于点C,且OC两点间的距离为3,x1 x2<0,|x1 |+|x2 |=4,点A,C在直线y2=-3x+t上.
(1)求点C的坐标;
(2)当y随着x的增大而增大时,求自变量x的取值范围;
(3)当抛物线y向左平移n(n>0)个单位,记平移后y随着x的增大而增大的部分为P,直线y2向下平移n个单位,当平移后的直线与P有公共点时,求2n²-5n的最小值.
解答过程见word版
中考2015年广东省广州市( )
某地区2013年投入教育经费2500万元,2015年投入教育经费3025万元.
(1)求2013年到2015年该地区投入教育经费的年平均增长率;
(2)根据(1)所得的年平均增长率,预计2016年该地区将投入教育经费多少万元.
(1)设2013年至2015年该地区投入教育经费的年平均增长率为x,
由题意得:2500(1+x)²=3025.
解得:x1=0.1,x2=-2.1(舍去)
所以,增长率为10%.
答:2013年至2015年该地区投入教育经费的年平均增长率为10%.
(2)由题意得:3025×(1+10%)=3327.5(万元)
答:2016年该地区将投入教育经费3327.5万元.
中考2015年广东省广州市( )
己知反比例函y=(m-7)/x的图象的一支位于第一象限.
(1)判断该函数图象的另一支所在的象限,并求m的取值范围;
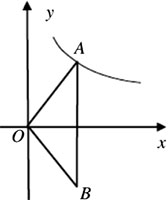
(2)如图,O为坐标原点,点A在该反比例函数位第于第一象限的图象上,点B与点A关于x轴对称,若△OAB的面积为6,求m的值.
(1)依题意,该函数图象的另一支在第三象限.
∵图象过第一、三象限,
∴m-7>0,解得m>7,
故所求m的取值范围为:m>7.
(2)设A(x,y),则B(x,-y),AB的距离为2y.
∵S△AOB=6,
∴1/2×2y×x=6,
∴xy=6,
∴m-7=6,
解得m=13.
故所求m的值为13.
中考2015年广东省广州市( )
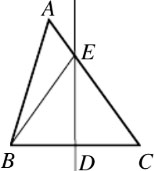
如图,△ABC中,DE是BC的垂直平分线,DE交AC于点E,连接BE,若BE=9,BC=12,则cosC=______.
2/3
∵DE是BC的垂直平分线,
∴CE=BE=9,CD=BD=1/2 BC=6,
∴cosC=CD/CE=6/9=2/3.
中考2015年广东省广州市( )
某水库的水位在5小时内持续上涨,初始的水位高度为6米,水位以每小时0.3米的速度匀速上升,则水库的水位高度y米与时间x小时0≤x≤5的函数关系式为__________.
y=6+0.3x

