中考2015年广东省广州市( )
解方程:5x=3(x-4)
方程去括号得:5x=3x-12,
移项合并得:2x=-12,
解得:x=-6.
中考2015年广东省广州市( )
已知2是关于x的方程x²-2mx+3m=0的一个根,并且这个方程的两个根恰好是等腰△ABC的两条边长,则△ABC的周长为【 】
A、10
B、14
C、10或14
D、8或10
14
∵2是关于x的方程x²-2mx+3m=0的一个根,
∴2²-4m+3m=0,解得:m=4,
∴原方程为:x²-8x+12=0,解得:x1=2,x2=6.
当6是腰时,2是底边,此时周长=6+6+2=14;
当6是底边时,2是腰,2+2<6,不成构成三角形,
∴三角形的周长是14.
中考2015年广东省广州市( )
已知a,b满足方程组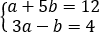 ,则a+b的值为【 】
,则a+b的值为【 】
A、-4
B、4
C、-2
D、2
4
①+②×5 得:16a=32,即 a=2,
把 a=2 代入①得:b=2,
则a+b=4.
中考2016年广东省广州市( )
分式方程1/2x=2/(x-3)的解是________.
x=-1
方程两边同乘以2x(x-3)得:x-3=4x,
解得:x=-1.
检验:当x=-1时,2x(x-3)≠0,
故原分式方程的解是x=-1.
中考2016年广东省广州市( )
定义新运算:a*b=a(1-b),若a,b是方程x²-x+1/4 m=0(m<0)的两根,则b*b-a*a的值为【 】
A、0
B、1
C、2
D、与m有关
0
由定义得:b*b-a*a=b(1-b)-a(1-a)=b-b²+a-a² ①.
∵a,b为方程x²-x+1/4 m=0的两根,
∴a²-a+1/4 m=0,b²-b+1/4 m=0,
代入①式可得:-(b²-b)+a²-a=-(-1/4 m)+(-1/4 m)=0.

