中考2015年广东省广州市( )
两名同学生进行了10次三级蛙跳测试,经计算,他们的平均成绩相同,若要比较这两名同学的成绩哪一位更稳定,通常还需要比较他们成绩的【 】
A、众数
B、中位数
C、方差
D、以上都不对
根据方差的意义:是反映一组数据波动大小、稳定程度的量;方差越大表明这组数据偏离平均数越大,即波动越大,反之也成立,故要判断哪一名学生的成绩比较稳定,通常需要比较这两名学生三级蛙跳测试成绩的方差。
中考2016年广东省广州市( )
某校为了提升初中学生学习数学的兴趣,培养学生的创新精神,举办“玩转数学”比赛,现有甲、乙、丙三个小组进入决赛,评委从研究报告、小组展示、答辩三个方面为各小组打分,各项成绩均按百分制记录,甲、乙、丙三个小组各项得分如下表:
小组 |研究报告 |小组展示| 答辩
甲 |91 |80 |78
乙| 81| 74| 85
丙 |79| 83| 90
(1)计算各小组的平均成绩,并从高分到低分确定小组的排名顺序;
(2)如果按照研究报告占40%,小组展示占30%,答辩占30%,计算各小组的成绩,哪个小组的成绩最高?
(1)甲:(91+80+78)÷3=83;
乙:(81+74+85)÷3=80;
丙:(79+83+90)÷3=84.
∴小组的排名顺序为:丙、甲、乙.
(2)甲:91x40%+80x30%+78X30%=83.8
乙:81x40%+74x30%+85X30%=80.1
丙:79x40%+83X30%+90X30%=83.5
∴甲组的成绩最高.
中考2017年广东省广州市( )
某班为了解学生一学期做义工的时间情况,对全班50名学生进行调查,按做义工的时间t(单位:小时),将学生分成五类:A类(0≤t≤2),B类(2<t≤4),C类(4<t≤6),D类(6<t≤8),E类(t>8).
绘制成尚不完整的条形统计图如图.根据以上信息,解答下列问题:
(1)E类学生有______人,补全条形统计图;
(2)D类学生人数占被调查总人数的______%;
(3)从该班做义工时间在0≤t≤4的学生中任选2人,求这2人做义工时间都在 2<t≤4中的概率.
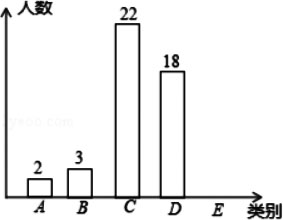
(1)E类:50-2-3-22-18=5(人),补全图如下:
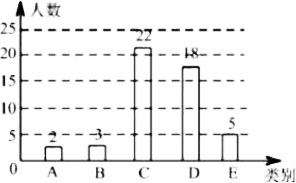
(2)D类:18÷50×100%=36%
(3)设这5人为:A1,A2,B1,B2,B3,有以下10种情况:
(A1,A2 ),(A1,B1 ),(A1,B2 ),(A1,B3 ),(A2,B1 ),(A2,B2 ),(A2,B3 ),(B1,B2 ),(B1,B2 ),(B2,B3),
其中,两人都在2<t≤4的情况有3种,
故所求概率为:P=3/10.
中考2017年广东省广州市( )
某6人活动小组为了解本组成员的年龄情况,作了一次调查,统计的年龄如下(单位:岁):12,13,14,15,15,15,这组数据中的众数,平均数分别为【 】
A、12,14
B、12,15
C、15,14
D、15,13
15出现次数最多,共3次,故众数为15;
平均数=(12+13+14+15+15+15)÷6=14.
中考2018年广东省广州市( )
随着移动互联网的快速发展,基于互联网的共享单车应运而生,为了解某小区居民使用共享单车的情况,某研究小组随机采访该小区的10位居民,得到这10位居民一周内使用共享单车的次数分别为:17,12,15,20,17,0,7,26,17,9.
(1)这组数据的中位数是______,众数是______;
(2)计算这10位居民一周内使用共享单车的平均次数;
(3)若该小区有200名居民,试估计该小区居民一周内使用共享单车的总次数.
(1)这组数据按大小排序可得:0,7,9,12,15,17,17,17,20,26.
中间两位数是15,17,则中位数为(15+17)/2=16.
这组数据中17出现的次数最多,所以众数为17.
(2)这组数据的平均数为:x ̅=(17+12+15+20+17+0+7+26+17+9)/10=14.
(3)若该小区有200名居民,该小区一周内使用共享单车的总次数大约为:
200×14=2800(次).

