中考2018年广东省广州市( )
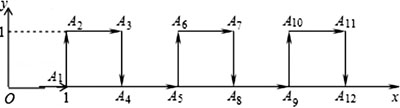
在平面直角坐标系中,一个智能机器人接到如下指令:从原点O出发,按向右,向上,向右,向下的方向依次不断移动,每次移动1m,其行走路线如图所示,第1次移动到A1,第2次移动到A2,…,第n次移动到An.则△OA2A2018的面积是【 】
A、504m²
B、1009/2m²
C、1011/2m²
D、1009m²
由图可得,每4步为一周期,每个周期横坐标向右移动2个单位,
∵2018/4=504⋯⋯2,504×2=108,
∴A2018 (1009,1),
又∵A2 (1,2),
∴S△OA2A2018=1/2×(2019-1)×1=504(m²).
中考2022年广东省广州市( )
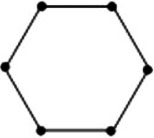
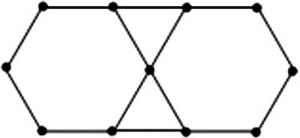
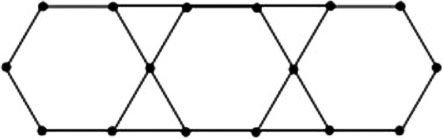
如图,用若干根相同的小木棒拼成图形,拼第1个图形需要6根小木棒,拼第2个图形需要14根小木棒,拼第3个图形需要22根小木棒,……,若按照这样的方法拼成的第n个图形需要2022根小木棒,则n的值为【 】
A、252
B、253
C、336
D、337
第1个图形为六边形,需要6根木棒;
从第2个图形开始,以后每增加1个六边形需要增加8个木棒,
所以,第n个图形需要的木棒数为:6+(n-1)×8=2022,
解得:n=253.
中考2019年广东省( )
如图1所示的图形是一个轴对称图形,且每个角都是直角,长度如图所示,小明按图2所示方法玩拼图游戏,两两相扣,相互间不留空隙,那么小明用9个这样的图形(图1)拼出来的图形的总长度是_____________________(结果用含a、b代数式表示).


a+8b
每个接触部分的相扣长度为(a-b),则下方空余部分的长度为a-2(a-b)=2b-a,
3个拼出来的图形有1段空余长度,总长度=2a+(2b-a)=a+2b;
5个拼出来的图形有2段空余长度,总长度=3a+2(2b-a)=a+4b;
7个拼出来的图形有3段空余长度,总长度=4a+3(2b-a)=a+6b;
9个拼出来的图形有4段空余长度,总长度=5a+4(2b-a)=a+8b.
中考2018年广东省( )
如图,已知等边△OA1 B1,顶点A1在双曲线y=√3/x(x>0)上,点B2的坐标为(2,0).过B1作B1 A2//OA1交双曲线于点A2,过A2作A2 B2//A1 B1交x轴于点B2,得到第二个等边△B1 A2 B2;过B2作B2 A3//B1 A2交双曲线于点A3,过A3作A3 B3//A2 B2交x轴于点B3,得到第三个等边△B2 A3 B3;以此类推,…,则点B6的坐标为______.

(2√6,0)
解答过程见word版
中考2015年广东省( )
观察下列一组数:1/3,2/5,3/7,4/9,5/11,…,根据该组数的排列规律,可推出第10个数是______.
12/21
解答过程见word版

