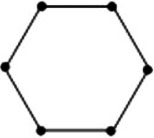
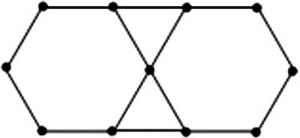
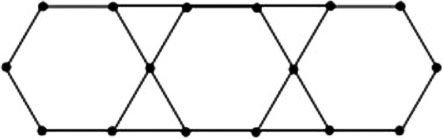
如图,用若干根相同的小木棒拼成图形,拼第1个图形需要6根小木棒,拼第2个图形需要14根小木棒,拼第3个图形需要22根小木棒,……,若按照这样的方法拼成的第n个图形需要2022根小木棒,则n的值为【 】
A、252
B、253
C、336
D、337
如图,用若干根相同的小木棒拼成图形,拼第1个图形需要6根小木棒,拼第2个图形需要14根小木棒,拼第3个图形需要22根小木棒,……,若按照这样的方法拼成的第n个图形需要2022根小木棒,则n的值为【 】



A、252
B、253
C、336
D、337
B
【解析】
第1个图形为六边形,需要6根木棒;
从第2个图形开始,以后每增加1个六边形需要增加8个木棒,
所以,第n个图形需要的木棒数为:6+(n-1)×8=2022,
解得:n=253.
设y=-k/(k+1) x+1/(k+1)与x轴,y轴交于A,B(k为正整数),记Sk为S△AOB在对应k时的大小,则S1+S2+⋯+S2023=________.
有九个方格,把1到9这些正整数均填入其中,要使任意相邻的三个格子的和为3的倍数,有______种填法.
有一数列(8项),首项与末项均为1,每一项与前一项比均为1或-1/2, 这种数列有______种.
用圆圈按如图所示的规律拼图案,其中第①个图案中有 2个圆圈,第②个图案中有 5 个圆圈,第③个图案中有8个圆圈,第④个图案中有 11 个圆圈,…,按此规律排列下去,则第⑦个图案中圆圈的个数为【 】
观察下列一组数:1/3,2/5,3/7,4/9,5/11,…,根据该组数的排列规律,可推出第10个数是______.