下列命题是真命题的个数有【 】
①垂直于半径的直线是圆的切线
②平分弦的直径垂直于弦
③若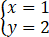 是方程x-ay=3的一个解,则a=-1
是方程x-ay=3的一个解,则a=-1
④若反例函数y=-3/x的图像上有两点(1/2,y1),(1,y2),则y1≤y2.
A、1个
B、2个
C、3个
D、4个
下列命题是真命题的个数有【 】
①垂直于半径的直线是圆的切线
②平分弦的直径垂直于弦
③若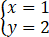 是方程x-ay=3的一个解,则a=-1
是方程x-ay=3的一个解,则a=-1
④若反例函数y=-3/x的图像上有两点(1/2,y1),(1,y2),则y1≤y2.
A、1个
B、2个
C、3个
D、4个
B
如图,已知反比例函数过A,B两点,A点坐标(2,3),直线AB经过原点,将线段AB绕点B顺时针旋转90°得到线段BC,则C点坐标为________.
在平面直角坐标系xOy中,若反比例函数y=k/x(k≠0)的图像经过点A(1,2)和点B(-1,m),则m的值为______.
若点A(x1,2),B(x2,-1),C(x3,4)都在反比例函数y=8/x的图像上,则x1,x2,x3的大小关系是【 】
根据物理学知识,在压力不变的情况下,某物体承受的压强p(Pa)是它的受力面积S(㎡)的反比例函数,其函数图象如图所示,当S=0.25㎡时,该物体承受的压强p的值为______Pa.
若反比例函数y=k/x(k≠0)的图像经过点(2,-3),则它的图像也一定经过的点是【 】
如图,点A是反比例函数y=3/x图象上任意一点,过点A分别作x轴,y轴的垂线,垂足为B,C,则四边形OBAC的面积为_______.