如图,△ABC内接于☉O中,BC=2,AB=AC,点D为弧AC上的动点,且cosB=√10/10.
(1)求AB的长度;
(2)如图(1),在点D运动的过程中,弦AD的延长线交BC延长线于点E,问AD·AE的值是否变化?若不变,请求出AD·AE 的值;若变化,请说明理由.
(3)如果(2),在点D的运动过程中,过A点作AH⊥BD,求证:BH=CD+DH.
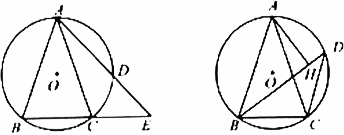
如图,△ABC内接于☉O中,BC=2,AB=AC,点D为弧AC上的动点,且cosB=√10/10.
(1)求AB的长度;
(2)如图(1),在点D运动的过程中,弦AD的延长线交BC延长线于点E,问AD·AE的值是否变化?若不变,请求出AD·AE 的值;若变化,请说明理由.
(3)如果(2),在点D的运动过程中,过A点作AH⊥BD,求证:BH=CD+DH.
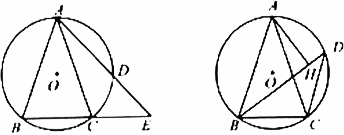
(1)过A作AF⊥BC,垂足为F,交⨀O于G,∵AB=AC,AF⊥BC,∴BF=CF,在Rt△ABF中,AB=BF/cosB=√10;(2)连接DG,∵AF⊥BC,BF=CF,∴AG为⨀O的直径,∴∠ADG=90°,∵∠DAG=∠FAE,∠ADG=∠AFE=90°,∴△ADG∼△AFE,∴AD/AF=AG/AE,∴AD⋅AE=AF⋅AG,∵AF=√(AB²-BC²)...
查看完整答案如图,AB与⊙O相切于点B,AO的延长线交⊙O于点C,连接BC,若∠A=40°,则∠C=________.
如图,AB是⨀O的直径,BC是⨀O的弦,先将 沿BC翻折交AB于点D,再将沿AB翻折交BC于点E.若=,设∠ABC=α,则α所在的范围是【 】
如图,ABAB是⨀O的直径,C,D是⨀O上两点,C是的中点.过点C作AD的垂线,垂足是E.连接AC交BD于点F.(1)求证:CE是⨀O的切线;(2)若DC/DF=,求cos∠ABD的值.
如图,四边形ABCD内接于⨀O,∠1=∠2,延长BC到点E,使得CE=AB,连接ED.(1)求证:BD=ED;(2)若AB=4,BC=6,∠ABC=60°,求tan∠DCB的值.
如图,FA、GB、HC、ID、JE是五边形ABCDE的外接圆的切线,则∠BAF+∠CBG+∠DCH+∠EDI+∠AEJ=______.
如图,已知P是⊙O外一点.用两种不同的方法过点P作⊙O的一条切线.要求:(1)用直尺和圆规作图;(2)保留作图的痕迹,写出必要的文字说明.
如图,AB是⊙O的直径,点C为圆上一点,AC=3,∠ABC的平分线交AC于点D,CD=1,则⊙O的直径为【 】
如图,AB为⨀O的弦,D,C为弧ACB的三等分点,AC//BE. (1)求证:∠A=∠E;(2)若BC=3,BE=5,求CE的长.
如图,在ΔABC中,点D,E分别是AB、AC边上的点,BD=CE,∠ABE=∠ACD,BE与CD相交于点F,求证:ΔABC是等腰三角形.
如图,在四边形ABCD中,AB=BC=BD.设∠ABC=α,则∠ADC______(用含α的代数式表示).
如图,等腰直角三角形ABC中,∠A=90°,BC=4.分别以点B、点C为圆心,线段BC长的一半为半径作圆弧,交AB、BC、AC于点D、E、F,则图中阴影部分的面积为________.
《九章算术》中有问题:1亩好田是300元,7亩坏田是500元,一人买了好田坏田一共是100亩,花费了10000元,问他买了多少亩好田和坏田?设一亩好田为x元,一亩坏田为y元,根据题意列方程组得【 】
如图,在点F处,看建筑物顶端D的仰角为32°,向前走了15米到达点E即EF=15米,在点E处看点D的仰角为64°,则CD的长用三角函数表示为【 】