初中数学-中考试题(北京市 2021年直线和圆)

问答题（2021年北京市）

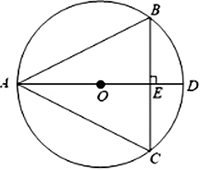
如图，⊙O是△ABC的外接圆，AD是⊙O的直径，AD⊥BC于点E.

(1)求证：∠BAD=∠CAD；

(2)连接并延长OB，交AC于点F，交⊙O于点G，连接GC.若⊙O的半径为5，OE=3,求GC和OF的长.

答案解析

(1) ∵AD是⨀O的直径，且AD⊥BC,∴(BD) ̂=(CD) ̂.∴∠BAD=∠CAD.(2)在Rt△BOE中，OB=5,OE=3,BE=4.∵AD是⨀O的直径，且AD⊥BC,∴BC=2BE=8...

查看完整答案

讨论

直线和圆

如图，AB为⨀O的弦，D,C为弧ACB的三等分点，AC//BE. (1)求证：∠A=∠E;(2)若BC=3,BE=5，求CE的长.

一根钢管放在V形架内，其横截面如图所示，钢管的半径是24cm，若ACB=60°，则劣弧AB的长是【】

如图，正方形ABCD的边长为4，点E是边BC上一点，且BE=3，以点A为圆心，3为半径的圆分别交AB,AD于点F,G,DF与AE交于点H.并与⨀A交于点K，连接HG,HC.给出下列四个结论，其中正确的有________（填写所有正确结论的序号）(1) H是FK的中点； (2) △HGD≅△HEC；(3) S△AHG:S△DHC=9:16; (4) DK=7/5

如图，PA,PB是⊙O的切线，A,B是切点.若∠P=50°，则∠AOB=________.

如图1，水平放置一个三角板和一个量角器，三角板的边AB和量角器的直径DE在一条直线上，AB=BC=6cm，OD=3cm，开始的时候BD=1cm，现在三角板以2cm/s 的速度向右移动.(1)当B与O重合的时候，求三角板运动的时间；(2)如图2，当AC与半圆相切时，求AD；(3)如图3，当AB和DE 重合时，连接CO交半圆于点F，连接并延长DF交CE于点G，求证：CF²=CG·CE.

如图，线段AB是⨀O的直径，弦CD⊥AB于点H，点M是(CBD) ̂上任意一点，AH=2,CH=4.(1)求⨀O的半径r的长度；(2)求sin∠CMD；(3)直线BM交直线CD于点E，直线MH交⊙O于点N，连接BN交CE于点F，求HE⋅HF的值.

如图所示，PA、PB分别与⊙O相切于、两点，点为⊙O上一点，连接AC、BC，若∠P=70°，则∠ACB的度数为【】

如图，在ΔABC中，∠C=90°，AD平分∠BAC交BC于点D，点O在AB上，以点O为圆心，OA为半径的圆恰好经过点D，分别交AC、AB于点E、F. （1）试判断直线BC与⊙O的位置关系，并说明理由；（2）若BD=2，AB=6，求阴影部分的面积（结果保留π）.

如图，A是⊙O上一点，BC是直径，AC=2，AB=4，点D在⊙O上且平分，则DC的长为【】

如图，⊙O是ΔABC的外接圆，其切线AE与直径BD的延长线相交于点E，且AE=AB. （1）求∠ACB的度数；（2）若DE=2，求⊙O的半径.

三角形

如图，每个小正方形边长均为1，则图中的三角形(阴影部分)与下图中△ABC相似的是【】

如图，△ABC与△DEF均为等边三角形，O为BC、EF的中点，则AD:BE的值为【】

如图，△ABC的内心在y轴上，点C的坐标为(2，0)，点B的坐标是(0，2)，直线AC的解析式为y=1/2 x-1，则tanA的值是______.

小明想测量一棵树的高度，他发现树的影子恰好落在地面和一斜坡上，如图，此时测得地面上的影长为8米，坡面上的影长为4米，已知斜坡的坡角为30°，同一时刻，根长为1米且垂直于地面放置的标杆在地面上的影长为2米，则树的高度为【】

如图， RT△ABC中∠C=90°，以斜边AB为边向外作正方形ABDE，且正方形对角线交于点O，连接OC，已知AC=5,OC=6，则另一直角边BC的长为________.

如图，在平面直角坐标系中，△AOB的边AO、AB的中点C、D的横坐标分别是1、4，则点B的横坐标是______.

如图，为了测量河对岸两点AB之间的距离，在河岸这边取点CD测得CD=80m，∠ACD=90°，∠BCD=45°，∠ADC=19°17'，∠BDC=56°19'，设A，B，C，D在同一平面内，求A，B两点之间的距离.(参考数据：tan19°17'≈0.35，tan56°19'≈1.50.)

如图，已知点O是△ABC的外心，∠A=40°，连结BO、CO则∠BOC的度数是【】

在△ABC中，∠ABC=90°，若AC=100,sinA=3/5，则AB的长是【】

如图，在△ABC中，点D、E分别是BC、AC的中点，AD与BE相交于点F，若BF=6，则BE的长是________.

圆

如图，已知AB=AC=5,BC=3，以A,B两点为圆心，大于1/2 AB的长为半径画圆弧，两弧相交于两点M,N，连接MN与AC相交于点D，则△BCD的周长为【】

如图1，在四边形ABCD中，AD// BC，∠DAB=90°，AB是⊙O的直径，CO平分∠BCD.（1）求证：直线CD与⊙O相切；（2）如图2，记（1）中的切点为E，P为优弧AE上一点，AD=1，BC=2.求tan⁡∠ APE的值.

如图，ΔABC是⊙O的内接正三角形，点O是圆心，点D，E分别在边AC，AB上，若DA=EB，则∠DOE的度数是_______度．

如图，AB为⊙O的直径，四边形ABCD内接于⊙O，对角线AC，BD交于点E，⊙O的切线AF交BD的延长线于点F，切点为A，且∠CAD=∠ABD．（1）求证：AD=CD；（2）若AB=4，BF=5，求sin⁡∠ BDC的值．

如图，在⊙O中，点A在弧BC上，∠BOC=100°,则∠BAC=__________.

如图，⊙O是△ABC的外接圆，AB是⊙O的直径，∠DCA=∠B. (1)求证:CD是⊙O的切线；(2)若DE⊥AB，垂足为E,DE交AC与点；求证:△DCF是等腰三角形.

如图，在Rt ΔABC中，∠ACB=90°，AC=2BC，分别以点A和B为圆心，以大于1/2 AB的长为半径作弧，两弧相交于点M和N，作直线MN，交AC于点E，连接BE，若CE=3，则BE的长为_________.

如图，在平行四边形ABCD中，AC是对角线，∠CAB=90°，以点A为圆心，以AB的长为半径作⊙A，交BC边于点E，交AC于点F，连接DE. （1）求证：DE与⊙A相切；（2）若∠ABC=60°，AB=4，求阴影部分的面积.

如图，在△ABC中，AB＝AC，以AB为直径的⊙O分别交AC、BC于点D、E，点F在AC的延长线上，且∠BAC＝2∠CBF．（1）求证：BF是⊙O的切线；（2）若⊙O的直径为4，CF＝6，求tan∠CBF．

一把直尺、60°的直角板和光盘如图摆放，A为60°角与直尺的交点，AB=3，则光盘的直径是【】