如图,在△ABC中,AB=AC,以AB为直径的⊙O分别交AC、BC于点D、E,点F在AC的延长线上,且∠BAC=2∠CBF.
(1)求证:BF是⊙O的切线;
(2)若⊙O的直径为4,CF=6,求tan∠CBF.
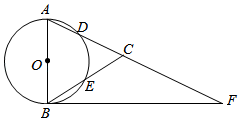
如图,在△ABC中,AB=AC,以AB为直径的⊙O分别交AC、BC于点D、E,点F在AC的延长线上,且∠BAC=2∠CBF.
(1)求证:BF是⊙O的切线;
(2)若⊙O的直径为4,CF=6,求tan∠CBF.

(1)证明:连接AE,∵AB是⊙O的直径,∴∠AEB=90°,∴∠1+∠2=90°.∵AB=AC,∴2∠1=∠CAB.∵∠BAC=2∠CBF,∴∠1=∠CBF∴∠CBF+∠2=90°即∠ABF=90°∵AB是⊙O的直径,∴直线BF是⊙O的切线;(2)解:过C作CH⊥BF于H,∵AB=AC,⊙O的直径为4,∴AC=4,∵...
查看完整答案如图所示,PA、PB分别与⊙O相切于 、 两点,点 为⊙O上一点,连接AC、BC,若∠P=70°,则∠ACB的度数为【 】
如图,A是⊙O上一点,BC是直径,AC=2,AB=4,点D在⊙O上且平分,则DC的长为【 】
如图,⊙C过原点,且与两坐标轴分别交于点A、点B,点A的坐标为(0,3),M是第三象限内上一点,∠BMO=120°,则⊙C的半径长为【 】
如图,AB是⊙O的直径,点C为圆上一点,AC=3,∠ABC的平分线交AC于点D,CD=1,则⊙O的直径为【 】
如图,AB为⨀O的弦,D,C为弧ACB的三等分点,AC//BE. (1)求证:∠A=∠E;(2)若BC=3,BE=5,求CE的长.
若一个扇形的圆心角为60°,面积为π/6 cm2,则这个扇形的弧长为_________cm(结果保留π).
下列四幅图中,能表示两棵树在同一时刻太阳光下的影子的图是【 】
如图是由 个小正方体组合成的几何体,该几何体的俯视图是【 】
下图是由一个长方体和一个圆锥组成的几何体,它的主视图是【 】
图(1)是一个长为2a,宽为2b(a>b)的长方形,用剪刀沿图中虚线(对称轴)剪开,把它分成四块形状和大小都一样的小长方形,然后按图(2)那样拼成一个正方形,则中间空余的部分的面积是【 】
如图,在矩形纸片ABCD中,AB=3,点E在边BC上,将△ABE沿直线AE折叠,点B恰好落在对角线AC上的点F处,若∠EAC=∠ECA,则AC的长是【 】