如图,射线AB和射线CB相交于点B,∠ABC=α(0°<α<180°),且AB=CB.点D是射线CB上的动点(点D不与点C和点B重合).作射线AD,并在射线AD上取一点E,使∠AEC=α,连接CE,BE.
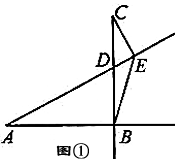
(1)如图①,当点D在线段CB上,α=90°时,请直接写出∠AEB的度数;
(2)如图②,当点D在线段CB上,α=120°时,请写出线段AE,BE,CE之间的数量关系,并说明理由;

(3)当α=120°,tan∠ DAB=1/3时,请直接写出CE/BE的值.
如图,射线AB和射线CB相交于点B,∠ABC=α(0°<α<180°),且AB=CB.点D是射线CB上的动点(点D不与点C和点B重合).作射线AD,并在射线AD上取一点E,使∠AEC=α,连接CE,BE.
(1)如图①,当点D在线段CB上,α=90°时,请直接写出∠AEB的度数;

(2)如图②,当点D在线段CB上,α=120°时,请写出线段AE,BE,CE之间的数量关系,并说明理由;

(3)当α=120°,tan∠ DAB=1/3时,请直接写出CE/BE的值.
(1)∠AEB=45°(2)AE= BE+CE,理由如下:在AD上截取AF=CE,连接BF,过点B作BH⊥EF于点H. ∵∠ABC=∠AEC、∠ADB=∠CDE∴180°-∠ABC-∠ADB=180°-∠AEC-∠CDE∴∠A=∠C∵BA=BC∴ΔABF≌ΔCBE(SAS )∴∠ABF=∠CBE,BF=BE∴∠ABF+∠FBD=∠CBE+∠FBD∴∠FBE=∠ABC∵∠ABC=120°...
查看完整答案如图,直线m//n,△ABC是等边三角形,顶点B在直线n上,直线m交AB于点E,交AC于点F,若∠1=140° ,则∠2的度数是【 】
如图,在矩形ABCD中,若AB=3,AC=5,AF/FC=1/4,则AE的长为________.
如图,直线a,b被直线c所截,A//b,∠1=60°.那么∠2=________°
如图,直线a,b被c,d所截,且a//b,则下列结论中正确的是【 】
如图,AB//CD,∠B=∠D,直线EF与AD,BC的延长线分别交于点E,F.求证:∠DEF=∠F.
已知关于x的一元二次方程x2-4mx+3m2=0.(1)求证:该方程总有两个实数根;(2)若m>0,且该方程的两个实数根的差为2,求m的值.