初中数学-中考试题(山西省 2022年直线)

问答题（2022年山西省）

如图，在矩形ABCD中，AC是对角线.

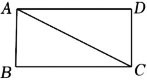
(1)实践与操作：利用尺规作线段AC的垂直平分线，垂足为点O，交边AD干点E，交边BC于点F(要求：尺规作图并保留作图痕迹，不写作法，标明字母).

(2)猜想与证明：试猜想线段AE与CF的数量关系，并加以证明.

答案解析

(1)作图如下： (2) AE=CF，证明如下：∵四边形ABCD是矩形，∴AD//BC，∴∠EAO=∠FCO,∠AEO=∠CFO，∵EF是AC的垂直平分线，∴AO=CO，∴△AOE≅△COF(AAS)...

查看完整答案

讨论

直线

《淮南子·天文训》中记载了一种确定东西方向的方法，大意是：日出时，在地面上点A处立一根杆，在地面上沿着杆的影子的方向取一点B，使B、A两点间的距离为10步(步是古代的一种长度单位)，在点B处立一根杆；日落时，在地面上沿着点B处的杆的影子的方向取一点C，使C、B两点间的距离为10步，在点C处立一根杆，取 CA的中点D，那么直线DB表示的方向为东西方向。(1)上述方法中，杆在地面上的影子所在直线及点A，B，C的位置如图所示。使用直尺和圆规，在图中作CA的中点D(保留作图痕迹)；(2)在图中，确定了直线DB表示的方向为东西方向，根据南北方向与东西方向互相垂直，可以判断直线CA表示的方向为南北方向，完成如下证明.证明：在△ABC中，BA=______，D是CA的中点，∴CA⊥DB(__________)(填推理的依据).∵直线DB表示的方向为东西方向，∴直线CA表示的方向为南北方向.

如图，射线OM、ON互相垂直，OA=8，点B位于射线OM的上方，且在线段OA的垂直平分线l上，连接AB，AB=5.将线段AB绕点O按逆时针方向旋转得到对应线段A′B′，若点B′恰好落在射线0N上，则点A′到射线ON的距离d=________.

下列长度的三条线段与长度为5的线段能组成四边形的是【】

如图是钉板示意图，每相邻4个钉点是边长为1个单位长的小正方形顶点，钉点A，B的连线与钉点 C，D的连线交于点E，则(1)AB与CD是否垂直?______(填是”或否")(2)AE=______.

如图是一张矩形纸板，顺次连接各边中点得到菱形，再顺次连接菱形各边中点得到一个小矩形．将一个飞镖随机投掷到大矩形纸板上，则飞镖落在阴影区域的概率是【】

不等式组的解集是【】

已知点A(x1,y1 )，B(x2,y2 )，C(x3,y3 )都在反比例函数y=k/x (k<0)的图像上，且x1<x2<0<x3，则y1，y2，y3的大小关系是【】

中国美食讲究色香味美，优雅的摆盘造型也会让美食锦上添花．图①中的摆盘，其形状是扇形的一部分，图②是其几何示意图（阴影部分为摆盘），通过测量得到AC=BD=12cm，C，D两点之间的距离为4cm，圆心角为60°，则图中摆盘的面积是【】

如图是一张长12cm，宽10cm的矩形铁皮，将其剪去两个全等的正方形和两个全等的矩形，剩余部分（阴影部分）可制成底面积24cm2是的有盖的长方体铁盒．则剪去的正方形的边长为______cm．

问题情境：如图①，点E为正方形ABCD内一点，∠AEB=90°，将RtΔABE绕点B按顺时针方向旋转90°，得到ΔCBE'（点A的对应点为点C），延长AE交CE'于点F，连接DE．猜想证明：（1）试判断四边形BE' FE的形状，并说明理由；（2）如图②，若DA=DE，请猜想线段CF与FE'的数量关系并加以证明；解决问题：（3）如图①，若AB=15，CF=3，请直接写出DE的长．

几何图形

各顶点都在方格纸的格点（横竖格子线的交错点）上的多边形称为格点多边形，它的面积S可用公式S＝a+1/2b﹣1（a是多边形内的格点数，b是多边形边界上的格点数）计算，这个公式称为“皮克（Pick）定理”．如图给出了一个格点五边形，则该五边形的面积S＝_______．

如图，已知∠1=70°，如果CD//BE，那么∠B的度数为【】

如图，PA与⊙O相切于A点，弦AB⊥OP，垂足为C，OP与⊙O相交于D点，已知OA=2，OP=4.(1)求∠POA的度数；(2)计算弦AB的长.

正八边形的每个内角为【】

如图，AB与⊙O相切于点B，AO的延长线交⊙O于点C，连接BC，若∠A=40°，则∠C=________.

如图1(左)，将一个正六边形各边延长，构成一个正六角星形 AFBDCE，它的面积为1，取△ABC和△DEF各边中点，连接成正六角星形 A1F1B1D1C1E1，如图2(中)中阴影部分，取△A1B1C1和△D1E1F1各边中点，连接成正六角星形A2F2D2C2E2，如图3(右)中阴影部分，如此下去…，则正六角星形 A4F4B4D4C4E4的面积为________.

如图，在平面直角坐标系中，点P的坐标为(-4，0)，⊙P的半径为2，将⊙P沿x轴向右平移4个单位长度得⊙P1.(1)画出⊙P1，并直接判断⊙P与⊙P1的位置关系；(2)设⊙P1与x轴正半轴，y轴正半轴的交点分别为A、B.求劣弧AB与弦AB围成的图形的面积(结果保留π).

如图，直角梯形纸片ABCD中，AD//BC，∠A=90°，∠C=30°，折叠纸片使BC经过点D，点C落在点E处，BF是折痕，且BF=CF=8.(1)求∠BDF的度数;(2)求AB的长.

如图，A、B、C是⊙O上的三个点，∠ABC=25°，则∠AOC=________.

如图，在▱ABCD中AD=2,AB=4,∠A=30°，以点A为圆心，AD的长为半径画弧交AB于点E，连接CE，则阴影部分的面积是__________（结果保留π）.

线

如图，射线AB和射线CB相交于点B，∠ABC=α（0°<α<180°），且AB=CB.点D是射线CB上的动点（点D不与点C和点B重合）.作射线AD，并在射线AD上取一点E，使∠AEC=α，连接CE，BE.（1）如图①，当点D在线段CB上，α=90°时，请直接写出∠AEB的度数；（2）如图②，当点D在线段CB上，α=120°时，请写出线段AE，BE，CE之间的数量关系，并说明理由；（3）当α=120°，tan⁡∠ DAB=1/3时，请直接写出CE/BE的值.

要得知作业纸上两相交直线AB，CD所夹锐角的大小，发现其交点不在作业纸内，无法直接测量，两同学提供了如下间接测量方案(如图1和图2)：对于方案I、Ⅱ，说法正确的是【】方案I①作一直线GH，交AB，CD于点E，F;②利用尺规作∠HFN=∠CFG;③测量∠AEH的大小即可.方案 Ⅱ①作一直线GH，交AB，CD于点E，F;②测量∠AEH和∠CFG的大小;③计算180°-∠AEH-∠CFG即可.

如图，直线a,b被直线c所截，A//b,∠1=60°.那么∠2=________°

已知关于x的一元二次方程x2-4mx+3m2=0.(1)求证：该方程总有两个实数根；(2)若m>0，且该方程的两个实数根的差为2，求m的值.

如图，Rt△ABC是一块直角三角板，其中∠C=90°,∠BAC=30°.直尺的一边DE经过顶点A，若DE//CB，则∠DAB的度数为【】

如图，AB//CD，∠B=∠D，直线EF与AD，BC的延长线分别交于点E，F.求证:∠DEF=∠F.

如图，直线a,b被c,d所截，且a//b，则下列结论中正确的是【】

如图，直线m//n，△ABC是等边三角形，顶点B在直线n上，直线m交AB于点E，交AC于点F，若∠1=140° ，则∠2的度数是【】

如图，在矩形ABCD中，若AB=3,AC=5,AF/FC=1/4，则AE的长为________.

如图，已知l1//l2//l3，相邻两条平行直线间的距离相等，若等腰直角△ABC的三个顶点分别在这三条平行直线上，则sinα的值是【】