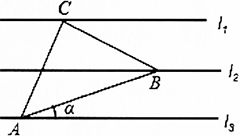
如图,已知l1//l2//l3,相邻两条平行直线间的距离相等,若等腰直角△ABC的三个顶点分别在这三条平行直线上,则sinα的值是【 】
A、1/3
B、6/17
C、√5/5
D、√10/10
如图,已知l1//l2//l3,相邻两条平行直线间的距离相等,若等腰直角△ABC的三个顶点分别在这三条平行直线上,则sinα的值是【 】

A、1/3
B、6/17
C、√5/5
D、√10/10
D如图,过点A作AD⊥l1于D,过点B作BE⊥l1于E,设l1,l2,l3间的距离为1. ∵∠CAD+∠ACD=90°,∠BCE+∠ACD=90°,∴∠CAD=∠BCE,在等腰直角△ABC中,AC=B...
查看完整答案如图,AB//CD,∠B=∠D,直线EF与AD,BC的延长线分别交于点E,F.求证:∠DEF=∠F.
已知关于x的一元二次方程x2-4mx+3m2=0.(1)求证:该方程总有两个实数根;(2)若m>0,且该方程的两个实数根的差为2,求m的值.
如图是钉板示意图,每相邻4个钉点是边长为1个单位长的小正方形顶点,钉点A,B的连线与钉点 C,D的连线交于点E,则(1)AB与CD是否垂直?______(填是”或否")(2)AE=______.
如图,Rt△ABC是一块直角三角板,其中∠C=90°,∠BAC=30°.直尺的一边DE经过顶点A,若DE//CB,则∠DAB的度数为【 】
如图,直线m//n,△ABC是等边三角形,顶点B在直线n上,直线m交AB于点E,交AC于点F,若∠1=140° ,则∠2的度数是【 】
如图,已知∠1=70°,如果CD//BE,那么∠B的度数为【 】
如图,在Rt△ABC中,∠C=90°.AF=EF.若∠CFE=72°.则∠B=______°.
如图,点O在直线AB上OC⊥OD.若∠AOC=120°,则∠BOD的大小为【 】.
为庆祝中国共产党建党100周年,某校用红色灯带制作了一个如图所示的正五角星(A,B,C,DE是正五边形的五个顶点),则图中∠A的度数是度______°.
如图,直线c与直线a、b都相交,若a//b,∠1=55°,则∠2=【 】
在△ABC中,AC=BC,∠B=38°,点D是边AB上一点,点B关于直线CD的对称点为B',当B'D//AC时,∠BCD的度数为______.