一根钢管放在V形架内,其横截面如图所示,钢管的半径是24cm,若ACB=60°,则劣弧AB的长是【 】
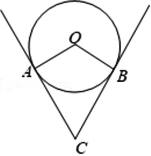
A、8πcm
B、16πcm
C、32πcm
D、192πcm
一根钢管放在V形架内,其横截面如图所示,钢管的半径是24cm,若ACB=60°,则劣弧AB的长是【 】

A、8πcm
B、16πcm
C、32πcm
D、192πcm
B由题意得:CA和CB分别与⨀O相切于点A和点B,∴OA⊥CA,OB⊥CB,∴∠OAC=∠OBC=90°,∵∠ACB=60°,∴∠AOB=120°,∴劣弧AB=(120π×24)/180=16π(cm...
查看完整答案如图,ΔABC是⊙O的内接正三角形,点O是圆心,点D,E分别在边AC,AB上,若DA=EB,则∠DOE的度数是_______度.
如图,AB是⨀O的直径,BC是⨀O的弦,先将 沿BC翻折交AB于点D,再将沿AB翻折交BC于点E.若=,设∠ABC=α,则α所在的范围是【 】
如图,ABAB是⨀O的直径,C,D是⨀O上两点,C是的中点.过点C作AD的垂线,垂足是E.连接AC交BD于点F.(1)求证:CE是⨀O的切线;(2)若DC/DF=,求cos∠ABD的值.
如图,四边形ABCD内接于⨀O,∠1=∠2,延长BC到点E,使得CE=AB,连接ED.(1)求证:BD=ED;(2)若AB=4,BC=6,∠ABC=60°,求tan∠DCB的值.
如图,FA、GB、HC、ID、JE是五边形ABCDE的外接圆的切线,则∠BAF+∠CBG+∠DCH+∠EDI+∠AEJ=______.
如图,已知P是⊙O外一点.用两种不同的方法过点P作⊙O的一条切线.要求:(1)用直尺和圆规作图;(2)保留作图的痕迹,写出必要的文字说明.
如图,在△ABC中,D,E分别为BC,AC上的点,将△CDE沿DE折叠,得到△FDE,连接BF,CF, ∠BFC=90°,若EF/AB,AB=4√3,EF=10,则AE的长为________.
如图,菱形ABCD中,点E是边CD的中点,EF垂直AB交AB的延长线于点F,若BF:CE=1:2,EF=√7,则菱形ABCD的边长是【 】
如图,已知四边形ABCD为等腰梯形,AD//BC,AB=CD,AD=√2,E为CD中点,连接AE,且AE=2√3,∠DAE=30°,作AF⊥AE交BC于F,则BF=【 】
把下列图标折成一个正方体的盒子,折好后与“中”相对的字是【 】
如图,已知a//b,直角三角板的直角顶角在直线b上,若∠1=60°,则下列结论错误的是【 】
如图,在扇形AOB中∠AOB=90°,正方形CDEF的顶点C是弧(AB) ̂的中点,点D在OB上,点E在OB 的延长线上,当正方形CDEF的边长为2√2时,阴影部分的面积为【 】
如图,已知线段AB,分别以A、B为圆心,大于1/2 AB为半径作弧,连接弧的交点得到直线l,在直线l上取一点C,使得∠CAB=25°,延长AC至M,求∠BCM的度数为【 】