如图,AB是⨀O的直径,BC是⨀O的弦,先将 沿BC翻折交AB于点D,再将
沿BC翻折交AB于点D,再将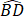 沿AB翻折交BC于点E.若
沿AB翻折交BC于点E.若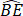 =
=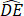 ,设∠ABC=α,则α所在的范围是【 】
,设∠ABC=α,则α所在的范围是【 】
A、21.9°<α<22.3°
B、22.3°<α<22.7°
C、22.7°<α<23.1°
D、23.1°<α<23.5°
如图,AB是⨀O的直径,BC是⨀O的弦,先将 沿BC翻折交AB于点D,再将
沿BC翻折交AB于点D,再将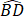 沿AB翻折交BC于点E.若
沿AB翻折交BC于点E.若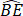 =
=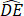 ,设∠ABC=α,则α所在的范围是【 】
,设∠ABC=α,则α所在的范围是【 】
A、21.9°<α<22.3°
B、22.3°<α<22.7°
C、22.7°<α<23.1°
D、23.1°<α<23.5°
B
如图,A是⊙O上一点,BC是直径,AC=2,AB=4,点D在⊙O上且平分,则DC的长为【 】
如图,⊙O是ΔABC的外接圆,其切线AE与直径BD的延长线相交于点E,且AE=AB. (1)求∠ACB的度数;(2)若DE=2,求⊙O的半径.
如图,ΔABC是⊙O的内接正三角形,点O是圆心,点D,E分别在边AC,AB上,若DA=EB,则∠DOE的度数是_______度.
如图,⊙O是△ABC的外接圆,AB是⊙O的直径,∠DCA=∠B. (1)求证:CD是⊙O的切线;(2)若DE⊥AB,垂足为E,DE交AC与点;求证:△DCF是等腰三角形.
如图,PA与⊙O相切于A点,弦AB⊥OP,垂足为C,OP与⊙O相交于D点,已知OA=2,OP=4.(1)求∠POA的度数;(2)计算弦AB的长.
一个等腰直角三角尺和一把直尺按如图所示的位置摆放,若∠1=20°,则∠2的度数是【 】
如图,我国某海域有A,B两个港口,相距80海里,港口B在港口A的东北方向,点C处有一艘货船,该货船在港口A的北偏西30°方向,在港口B的北偏西75°方向,求货船与港口A之间的距离.(结果保留根号)
如图,AB是⊙O的直径,PA切⊙O于点A,线段PO交⊙O于点C.连接BC,若∠P=36°,则∠B=_______.
如图,已知∠1=70°,如果CD//BE,那么∠B的度数为【 】
如图所示,△ABC中,AC=AD=BD,∠DAC=80°,则∠B的度数是【 】
如图,在点F处,看建筑物顶端D的仰角为32°,向前走了15米到达点E即EF=15米,在点E处看点D的仰角为64°,则CD的长用三角函数表示为【 】