在平面直角坐标系xOy中，⊙O的半径为1.对于点A和线段BC，给出如下定义：若将线段BC绕点A旋转可以得到⊙O的弦B'C'(B',C'分别是BC的对应点)，则称线段BC是⊙O的以点A为中心的“关联线段”.

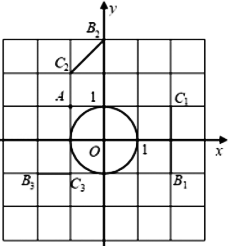
(1)如图，点A，B₁，C₁，B₂，C₂，B₃，C₃的横、纵坐标都是整数，在线段B₁C₁，B₂C₂， B₃C₃中，⊙O的以点A为中心的“关联线段”是__________;

(2)△ABC是边长为1的等边三角形，点A(0，t)，其中t≠0.若BC是⊙O的以点A为中心的“关联线段”，求t的值；

(3)在△ABC中，AB=1，AC=2.若BC是△O的以点A为中心的“关联线段”，直接写出OA的最小值和最大值，以及相应的BC长。