如图,ABAB是⨀O的直径,C,D是⨀O上两点,C是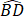 的中点.过点C作AD的垂线,垂足是E.连接AC交BD于点F.
的中点.过点C作AD的垂线,垂足是E.连接AC交BD于点F.

(1)求证:CE是⨀O的切线;
(2)若DC/DF=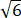 ,求cos∠ABD的值.
,求cos∠ABD的值.
如图,ABAB是⨀O的直径,C,D是⨀O上两点,C是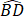 的中点.过点C作AD的垂线,垂足是E.连接AC交BD于点F.
的中点.过点C作AD的垂线,垂足是E.连接AC交BD于点F.

(1)求证:CE是⨀O的切线;
(2)若DC/DF=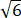 ,求cos∠ABD的值.
,求cos∠ABD的值.
(1)连接OC交BD于点G.∵ 点C是的中点,∴ 由圆的对称性得OC垂直平分BD.∵ AB是⊙O的直径,∴∠ADB=90°,∴∠EDB=90°.∵ CE⊥AE, ∴∠E=90°.∴ 四边形EDGC是矩形,∴∠ECG=90°.∴ CE是⨀O的切线.(2)连接BC,设FG=x,OB=r.∵ DC/DF=,∴设DF=t,DC= t.由(1)得BC=CD= t,BG=GD=x+t.∵ AB是⊙O的直径,∴∠ACB=90°.∴ ∠BCG+...
查看完整答案