某款“不倒翁”(左图)的主视图(右图)中,PA,PB分别与(AMB) ̂所在圆相切于点A,B.若该圆半径是9cm,∠P=40°,则(AMB) ̂的长是【 】
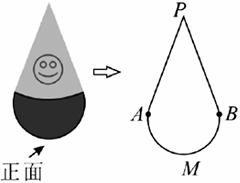
A、11πcm
B、11/2 πcm
C、7πcm
D、7/2 πcm
某款“不倒翁”(左图)的主视图(右图)中,PA,PB分别与(AMB) ̂所在圆相切于点A,B.若该圆半径是9cm,∠P=40°,则(AMB) ̂的长是【 】

A、11πcm
B、11/2 πcm
C、7πcm
D、7/2 πcm
A
【解析】
如图,
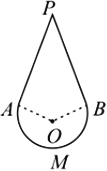
∵PA,PB分别与(AMB) ̂所在圆相切于点A,B
∴∠PAO=∠PBO=90°
又∵∠P=40°
∴∠AOB=140°
∴(AMB) ̂=(360-140)/180×π×9=11π(cm)
如图所示,PA、PB分别与⊙O相切于 、 两点,点 为⊙O上一点,连接AC、BC,若∠P=70°,则∠ACB的度数为【 】
如图,A是⊙O上一点,BC是直径,AC=2,AB=4,点D在⊙O上且平分,则DC的长为【 】
如图,⊙O是ΔABC的外接圆,其切线AE与直径BD的延长线相交于点E,且AE=AB. (1)求∠ACB的度数;(2)若DE=2,求⊙O的半径.
如图,ΔABC是⊙O的内接正三角形,点O是圆心,点D,E分别在边AC,AB上,若DA=EB,则∠DOE的度数是_______度.
如图,⊙O是△ABC的外接圆,AB是⊙O的直径,∠DCA=∠B. (1)求证:CD是⊙O的切线;(2)若DE⊥AB,垂足为E,DE交AC与点;求证:△DCF是等腰三角形.
如图,已知AB=AC=5,BC=3,以A,B两点为圆心,大于1/2 AB的长为半径画圆弧,两弧相交于两点M,N,连接MN与AC相交于点D,则△BCD的周长为【 】
如图所示,若用半径为8,圆心角为120°的扇形围成一个圆锥的侧面(接缝忽略不计),则这个圆锥的底面半径是_________.
如图所示的木制活动衣帽架是由三个全等的菱形构成,根据实际需要可以调节AE间的距离.若AE间的距离调节到60cm ,菱形的边长AB=20cm ,则∠DAB的度数是【 】
若一个扇形的圆心角为60°,面积为π/6 cm2,则这个扇形的弧长为_________cm(结果保留π).
如图,从一块半径为1m 的圆形铁皮上剪出一个圆周角为120°的扇形ABC,如果将剪下来的扇形围成一个圆锥,则该圆锥的底面圆的半径为_________m.
如图,在⊙O中,点A在弧BC上,∠BOC=100°,则∠BAC=__________.
如图,PA与⊙O相切于A点,弦AB⊥OP,垂足为C,OP与⊙O相交于D点,已知OA=2,OP=4.(1)求∠POA的度数;(2)计算弦AB的长.
如图,AB与⊙O相切于点B,AO的延长线交⊙O于点C,连接BC,若∠A=40°,则∠C=________.
如图,A、B、C是⊙O上的三个点,∠ABC=25°,则∠AOC=________.
如图,在⊙O中,圆心角∠AOB=120°,弦AB=2cm,则OA=_______cm.
如图,⊙C过原点,且与两坐标轴分别交于点A、点B,点A的坐标为(0,3),M是第三象限内上一点,∠BMO=120°,则⊙C的半径长为【 】
如图,AB是⨀O的直径,BC是⨀O的弦,先将 沿BC翻折交AB于点D,再将沿AB翻折交BC于点E.若=,设∠ABC=α,则α所在的范围是【 】